Apophenia als Apologet der Hellsichtigkeit an den Kapitalmärkten.
Inhaltsverzeichnis.
1. Einführung.
2. Paradigma: linear vs nichtlinear.
3. Methode zur Modellierung der Wertdynamik am Finanzmarkt.
3.1. Vorwort.
3.2. Der Finanzmarkt ist die NDASS.
3.3. Die Kosten sind eine Funktion der Zeit: P = N (T).
3.4. Fraktale und fraktale Struktur.
3.5. Die Reihenfolge, Arten und Typen von Fraktalen.
3.6. Grundlegendes Fraktal.
3.7. Gesamtansicht der fraktalen Struktur.
3.8. Grundlegende fraktale Dynamik.
3.9. Beschreibung der fraktalen Struktur.
3.10. Bestimmung von Ordnung und Chaos.
3.11. Die Reihenfolge der Fraktale.
3.12. Nummerierung von Fraktalen.
3.13. Bestimmung von Extremumpunkten.
3.14. Arten und Typen von Fraktalen.
3.15. 15 Fraktale:
3.15.1. Fraktale des 1. Art;
3.15.2. Fraktale des 2. Art;
3.15.3. Fraktale des 3. Art.
3.16. Proportionen zwischen fraktalen Segmenten.
3.17. Das Alphabet der Niro-Attraktoren.
3.18. Verzweigungspunkt und Freiheitsgrade.
3.19. Kosten und Zeitintervalle.
3.20. Das Wesen der Modellierungsmethode.
4. Modell der zukünftigen Dynamik der Dow Jones Indexwerte.
5. Fazit.
Dieses Artikel beschreibt eine Methode zur Modellierung der zukünftigen Wertdynamik von Finanzanlagen.
Die Methode basiert auf Chaostheorie und fraktaler Geometrie.
Apophenie ist die Fähigkeit, Strukturen, Verbindungen und Regelmäßigkeiten zu sehen, wo sie nicht offensichtlich oder verborgen sind.
Im Universum ist alles natürlich. Regelmäßigkeit ist überall und in allem ständig vorhanden.
Regelmäßigkeit ist immer verborgen, daher der Satz "Hier gibt es keine Regelmäßigkeit!" sagt nicht über seine Abwesenheit aus, sondern darüber, dass das Muster noch nicht entdeckt wurde. Das Muster wird nur während seiner Suche gefunden.
Der Artikel beschreibt die Möglichkeit, die Dynamik des Finanzmarktes vorherzusagen und die Methode zur Modellierung der Dynamik von Notierungen von Finanzanlagen.
Bei der Hellsichtigkeit des Finanzmarktes geht es nicht um Überfähigkeit aus der Kategorie des Übernatürlichen. Es ist klar, die zukünftige Dynamik der Kurse für Währungen, Aktien, Anleihen, Futures und Optionen für jeden zu sehen.
Die Aufgabe, die Dynamik von Zitaten zu modellieren, ist nicht komplizierter als die Aufgabe, eine quadratische Gleichung zu lösen. Die Modellierungsmethode setzt ebenso wie die Methode zum Finden der Wurzeln einer quadratischen Gleichung die Ausführung eines verständlichen Handlungsalgorithmus voraus.
Eine klare Vision der Dynamik des Finanzmarktes folgt aus einer klaren Vision in den chaotischen Wertschwankungen von Finanzanlagen der regulären Dynamik, die nach einer bestimmten Ordnung strukturiert ist.

1. Einführung.
Die im letzten Jahrhundert entwickelte Wirtschaftstheorie mit dem vorherrschenden linearen Paradigma ist nicht in der Lage, die in der Wirtschaft ablaufenden Prozesse zu erklären und ihre zukünftige Entwicklung vorherzusagen, so dass die Fragen des Preisbildungsmechanismus an den Kapitalmärkten unbeantwortet bleiben.
Die Wertdynamik auf dem Finanzmarkt, die plötzlichen und starken Schwankungen unterliegt, wird weder durch die Effizienzmarkthypothese noch durch andere Hypothesen von Ökonomen der traditionellen klassischen Schule erklärt.
Studien über Kapitalmärkte im Kontext ihrer Funktionsweise zwingen uns, nach neuen Ansätzen zu suchen, um einen Preismechanismus zu finden, bei dem wissenschaftliche Erkenntnisse mit der objektiven Realität übereinstimmen.
Die Notwendigkeit, ein neues Paradigma einzuführen, wird immer offensichtlicher, in dem die Theorie die zukünftige Wertdynamik am Finanzmarkt erklären würde und die objektive Realität dies bestätigen würde. Genau über eine solche Theorie, die den Mechanismus beschreibt, der den Wert auf dem Finanzmarkt in Dynamik bringt, wird in diesem Artikel diskutiert.
Nichtlineare dynamische Systeme, Chaostheorie, fraktale Geometrie, Synergetik – das sind die Bereiche des wissenschaftlichen Denkens, die in Bezug auf die Wertdynamik am Finanzmarkt erklären und verstehen, was passiert ist, was passiert und was passieren wird mit der Dynamik der Notierungen von Finanzinstrumenten.
Die Wertdynamik von Finanzinstrumenten, die sich im elektronischen Handel und im Börsenhandel abzeichnet, ist nicht chaotisch, da sie einem bestimmten Gesetz unterliegt, das ihre Vorhersage ermöglicht. Dementsprechend ist auch die Dynamik des gesamten Finanzmarktes vorhersehbar.
Das auf diesem Gesetz basierende Prognoseverfahren ermöglicht es, die zukünftige Wertentwicklung von Finanzanlagen zu simulieren und auf Basis der erarbeiteten Modelle effektive Anlageentscheidungen durch tatsächliches Marktrisikomanagement zu treffen.
Im weiteren Sinne kann man sagen, dass die Prognosemethode eine Computertechnologie zur Modellierung des Verhaltens nichtlinearer Prozesse in sozialen dynamischen Systemen ist, die Finanzmärkte als Teil der Wirtschaft sind.
Die Modellierung der Dynamik des Finanzmarktes geht davon aus, basierend auf der Analyse von Zeitreihen die Modelle der zukünftigen Dynamik der Notierungen von Finanzinstrumenten (Währungen, Aktien, Indizes, Derivate etc.) Wählen Sie die wahrscheinlichsten Entwicklungsszenarien aus.
Das Modell der zukünftigen Wertdynamik eines finanziellen Vermögenswerts ist eine Beschreibung der wahrscheinlichsten Kursbewegungsverläufe auf dem Chart, die zum Zeitpunkt der Erstellung relevant sind.
2. Paradigma: linear vs nichtlinear.
Ein Paradigma ist ein spekulatives Modell, das es Ihnen ermöglicht, Phänomene in einem globalen Aspekt zu betrachten.
Zunächst betrachten wir kurz die allgemein anerkannte Theorie der Kapitalmärkte in einem linearen Paradigma, zeigen ihre Vor- und Nachteile auf und skizzieren dann die Überlegenheit des nichtlinearen Paradigmas zur Beschreibung der Dynamik des Finanzmarktes.
Der Vorteil eines linearen Modells ist seine Einfachheit, so dass es einfacher ist, mit linearen Modellen zu arbeiten und die Gefahr von Berechnungsfehlern, die in seinen Grenzen liegen, zu ignorieren.
Um die Finanzmärkte verständlicher zu machen, haben Ökonomen Erklärungsmodelle entwickelt, die die Realität nicht vollständig widerspiegeln. Mit Hilfe einiger vereinfachender Annahmen über das Anlegerverhalten wurde ein allgemeines analytisches Modell in einem linearen Paradigma erstellt, das nicht gut funktioniert, aber einige Phänomene und Prozesse in der Wirtschaft erklärt und dabei vieles unklar und unerklärlich lässt.
So zeigt sich beispielsweise, dass Konjunkturprognosen nur eine begrenzte empirische Aussagekraft haben, d. h. die konstruierten ökonomischen Modelle der Zukunft spiegeln die Realität nur in einem kurzen Zeitintervall wider, da eine kleine Änderung nur einer Variablen große Auswirkungen auf die Zukunft hat Ergebnis.
Darüber hinaus wird zunehmend entdeckt, dass sich der Wert auf dem Finanzmarkt tatsächlich nicht so verhält, wie es die Theorie der Random Walks erfordert, die Ökonomen in ihren Berechnungen verwenden.
Es gibt noch viele weitere große Preissprünge an den Märkten, die durch die Ausnahme von der Regel in Form von Rauscheffekten zu erklären sind.
In der Phase der Entstehung und Entwicklung der Ökonometrie als Wissenschaft wurde von der Entstehung von Möglichkeiten zur genauen Prognose der Entwicklung wirtschaftlicher Prozesse ausgegangen, um Wirtschaftskrisen oder deren negative Folgen zu verhindern und zu vermeiden.
Konjunkturprognosen werden heute oft verspottet und lächerlich gemacht, weil über ihre Vorhersagewirkung nicht gesprochen werden muss.
Woher kommen Fehler, wo liegen sie und warum sieht die moderne Wirtschaftstheorie Krisen in der Wirtschaft nicht voraus, um sich richtig darauf vorzubereiten? Was sind die Probleme?
Erstens ist eines der Probleme das Konzept des Gleichgewichts, das in der Wirtschaftstheorie existiert. Der ökonometrische Ansatz geht davon aus, dass sich das System ohne äußere Einflüsse in Ruhe befindet, also in einem Gleichgewichtszustand, in dem sich alles ausgleicht. Zum Beispiel ist Angebot gleich Nachfrage.
Die aufkommenden exogenen Faktoren, die das System stören, bringen es aus dem Gleichgewicht. Das System reagiert auf die Störung und kehrt linear und sofort in die Gleichgewichtslage zurück, da es stets nach Gleichgewicht strebt und keine Unwucht akzeptiert. Um das Gleichgewichtskonzept aufrechtzuerhalten, wurde das Konzept eines effizienten Marktes eingeführt, nach dem alle Vermögenswerte fair bewertet werden, d.h. unter Nutzung aller Informationen, die ausnahmslos allen Marktteilnehmern zur Verfügung stehen, die zudem Risiken bei der Anlagetätigkeit abgeneigt sind.
All diese Annahmen über das Gleichgewicht, über die allgemeine Verfügbarkeit von Informationen, über das Ignorieren von Risiken, gelinde gesagt, sind jedoch weit hergeholt und entsprechen nicht der Realität.
Die Marktwirtschaft ist ein sich entwickelndes System, Versuche zu kontrollieren, zu verwalten und im Gleichgewicht zu halten, sind zum Scheitern verurteilt. Wirtschaftskrisen, die uns regelmäßig wie Schnee auf den Kopf fallen, sind dafür eine gute Bestätigung.
Zweitens ist Zeit ein wichtiges Problem für ein ökonometrisches Weltbild. Die Ökonometrie ignoriert die Zeit, d.h. Volkswirtschaften und Märkte haben bei diesem Ansatz keine oder nur eine sehr begrenzte Erinnerung an die Vergangenheit. Im besten Fall erkennt die Ökonometrie kurzes Gedächtnis. Es wird angenommen, dass sich Gedächtniseffekte schnell auflösen.
Die Vorstellung, dass ein Ereignis die Zukunft unbegrenzt beeinflussen kann, ist der Ökonometrie fremd. Die reale Sachlage weist auf das Gegenteil hin. Absolut alle Ereignisse, die sich in der Vergangenheit jemals ereignet haben, unabhängig von der Verjährung, haben Einfluss auf die Entwicklung der Wirtschaft und die Dynamik des Finanzmarktes in der Gegenwart und Zukunft – auch vor einem Tag, sogar vor einer Woche, sogar vor einem Monat, sogar vor Jahren, Jahrzehnten und Jahrhunderten.
Die Kapitalmarkttheorie in einem linearen Paradigma basiert auf den folgenden Konzepten:
1. Rationale Anleger.
Rationale Anleger streben eine durchschnittliche Rendite bei einem Risiko an, das als Standardabweichung gemessen wird. Bevorzugt werden Vermögenswerte, die die höchste erwartete Rendite für ein bestimmtes Risikoniveau bieten. Anleger sind risikoscheu und vermeiden es auf jede erdenkliche Weise.
2. Ein effizienter Markt.
Ein effizienter Markt bedeutet, dass sich Informationen unmittelbar in Preisen niederschlagen, die von allen gleichberechtigten Marktteilnehmern gebildet werden.
3. Zufällige Spaziergänge.
Entsprechend den obigen beiden Konzepten folgen Preise und als Folge des Gewinns einem Random Walk, d.h. ihre Wahrscheinlichkeitsverteilung ist normal, was die Möglichkeit bedeutet, das Gesetz der Normalverteilung einer Zufallsvariablen anzuwenden und den mathematischen Erwartungswert mit der Varianz zu berechnen.
Das lineare Paradigma geht davon aus, dass Anleger linear auf Informationen reagieren, diese unmittelbar nach Erhalt verwenden und nicht erwarten, dass sie sich in einer Reihe nachfolgender Ereignisse anhäufen. Die lineare Sichtweise folgt dem Konzept des rationalen Investors, der besagt, dass Informationen aus der Vergangenheit bereits diskontiert und in Preisen widergespiegelt wurden. Somit impliziert das lineare Paradigma, dass die Gewinne ungefähr normal und unabhängig sein sollten.
Das nichtlineare Paradigma berücksichtigt alle möglichen Reaktionen von Anlegern auf Informationen, sowohl lineare als auch nichtlineare, was die Anzahl der möglichen Szenarien für die Entwicklung der Situation erhöht.
Die Ergebnisse von Studien zu Zeitreihen verschiedener finanzieller Vermögenswerte zeigen, dass die Preise keiner Normalverteilung folgen, daher ist es unmöglich, die Theorie der Random Walks auf sie anzuwenden und die Methoden der statistischen Analyse in Berechnungen zu verwenden.
Übermäßige Wertvolatilität in den Märkten Herausforderungen:
• die Idee rationaler Investoren;
• ein Konzept, das besagt, dass Markteffizienz durch eine Vielzahl von Marktteilnehmern erreicht werden kann.
Random Walk ist notwendig, um statistische Analysen auf Zeitreihen von Preisänderungen anzuwenden, damit eine Portfoliotheorie existiert. Ohne eine Normalverteilung in einem linearen Paradigma sind theoretische und empirische Berechnungen bedeutungslos.
Die Theorie des effizienten Marktes basiert auf dem Postulat der Rationalität der Anleger. Die Rationalität wird durch die Preisgestaltung auf der Grundlage aller verfügbaren Informationen bestimmt. Rationalität bedeutet auch, dass Anleger risikoscheu sind. Aber sind Menschen in ihrer Gesamtheit rational, wenn wir von dieser Definition von Rationalität ausgehen? Natürlich nicht!
Überlegen Sie, wie Menschen reagieren, wenn sie vor der Wahl stehen, einen Verlust oder einen Gewinn zu erzielen.
Die allgemein anerkannte Theorie besagt, dass Anleger risikoscheu sind. Und wenn jemand ein großes Risiko eingeht, dann muss dieses Risiko durch die Möglichkeit eines großen Gewinns ausgeglichen werden.
Studien aller Art zeigen, dass Menschen, wenn Verluste akzeptabel sind, Risiken eingehen und eher zu Spielern als zu rationalen Anlegern werden.
Nehmen wir ein Beispiel, um die Veränderung der Risikobereitschaft zu zeigen.
Angenommen, ein Investor hat die Wahl zwischen:
1) Garantierter Gewinn von $ 85'000 oder
2) 85% Gelegenheit, $ 100'000 zu verdienen und 15% Gelegenheit, nichts zu verdienen.
Die meisten Anleger werden eine garantierte Rendite von 85.000 US-Dollar bevorzugen, obwohl die erwartete Rendite in beiden Fällen mit 85.000 US-Dollar gleich ist. Diese Wahl bestätigt die Risikoaversion der Anleger.
Wenn Sie anbieten, eine Wahl zu treffen zwischen:
1) Garantierter Verlust von $ 85'000 oder
2) 85% Wahrscheinlichkeit $ 100'000 zu verlieren und 15% - nichts zu verlieren
dann gehen die Menschen trotz des gleichen erwarteten Verlustes in beiden Fällen bereits Risiken ein und die Chance, Verluste zu vermeiden, ist der Chance, einen garantierten Verlust zu erleiden, vorzuziehen, selbst wenn die Wahrscheinlichkeit dieses zukünftigen Verlustes hoch ist. Der Wortlaut hat sich geändert und Anleger gehen jetzt Risiken ein.
Die effiziente Markttheorie geht auch davon aus, dass alle Anleger den gleichen Anlagehorizont haben. Diese Annahme ist notwendig, damit die erwarteten Renditen vergleichbar sind. Aber das ist bekanntlich in Wirklichkeit nicht der Fall.
Wenn sich die Möglichkeit bietet, jetzt 10'000 $ oder 10'500 $ in einem Monat zu erhalten, werden die meisten Anleger es vorziehen, jetzt 10'000 $ zu erhalten. Wenn Anlegern jedoch $ 10'000 in einem Jahr oder $ 10'500 in 13 Monaten geboten werden, dann werden die meisten Anleger einen längeren Zeitraum wählen, um $ 10'500 zu erhalten. Auch dies passt nicht zum rationalen Anlegermodell.
Besonderes Augenmerk sollte darauf gelegt werden, wie sich Menschen unter Bedingungen der Unsicherheit verhalten. Die Rationalitätshypothese der Anleger besagt, dass ihre subjektiven Risikoeinschätzungen gleich sind. Die überwältigende Mehrheit der Anleger neigt jedoch dazu, ihre Einschätzungen und Prognosen zu überschätzen. Das menschliche Gehirn ist so konzipiert, dass es nach Erhalt spärlicher Informationen mit hoher Sicherheit Entscheidungen trifft.
Vertrauen in die Entscheidungsfindung angesichts von Unsicherheit ist eine Standardsituation für Anleger. Übermäßiges Selbstvertrauen kann jedoch dazu führen, dass wichtige Informationen ignoriert werden, die von anderen verwendet werden könnten. Folglich neigen Anleger aufgrund ihrer subjektiven Einschätzung dazu, einzelnen Konjunkturszenarien eine höhere Wahrscheinlichkeit zuzuschreiben, als dies durch reale Fakten gerechtfertigt ist.
Wenn also beispielsweise in einem Wirtschaftsszenario 60 % Wachstum, 30 % kein Wachstum und 10 % Rezession zugeordnet werden, dann wird ein Anleger, der vom Wachstumsszenario überzeugt ist, diese Wahrscheinlichkeit in Wirklichkeit lieber auf 90 % erhöhen. , und lassen Sie 10% für ein schleppendes Wachstum, um nicht zu selbstbewusst zu wirken. Was die Rezession angeht, wird gesagt, dass dies im Moment nicht möglich ist.
Beobachtungen von Anlegern zeigen, dass sie nicht reagieren und den an den Märkten begonnenen Trends nicht folgen, bis diese Trends klar manifestiert und etabliert sind. Anleger extrapolieren die an den Märkten auftretenden Phänomene und Ereignisse nicht für einen bestimmten Zeitraum ihrer Entwicklung, wonach sie Entscheidungen treffen, die durch die angesammelten Informationen bedingt sind, die bis zu einem bestimmten Zeitpunkt ignoriert werden. Dieses Verhalten von Anlegern unterscheidet sich grundlegend von den beabsichtigten Handlungen rationaler Anleger, die sich sofort von allen neuen Informationen leiten lassen sollten.
Anleger neigen dazu, sich in ihren eigenen Prognosen zu sicher zu sein, sodass sie wichtige Informationen ignorieren, wenn sie nicht mit ihrer Meinung übereinstimmen. Anleger geben ihre Prognosen nicht auf, bis sie genügend Informationen über eine Änderung der Situation erhalten.
Wenn Anleger auf diese Weise reagieren, kann der Markt nicht effizient sein, da sich nicht alle Informationen in Marktpreisen widerspiegeln. Vieles bleibt in diesem Fall in den Preisen unberücksichtigt, und die Reaktion der Anleger auf die eingetretenen Ereignisse kommt später, und von Linearität muss nicht gesprochen werden.
Wenn einzelne Anleger nicht dazu neigen, so rational zu sein, gibt es keinen Grund zu der Annahme, dass dies nicht in der gesamten Anlegergemeinschaft der Fall ist.
Wenn Anleger Informationen ignorieren, bis Trends festgestellt sind, und sie dann unter Berücksichtigung aller gesammelten Informationen bei Entscheidungen verwenden, bedeutet dies, dass die Reaktion auf Informationen nicht linear ist. Sobald die Menge der angesammelten Informationen ein bestimmtes kritisches Niveau überschreitet, beginnt sofort ihr gesamter kumulativer Einfluss zu wirken, der vorher keine Folgen hatte. Dies spricht vom direkten Einfluss der Vergangenheit auf die Gegenwart und damit von der völligen Inkonsistenz der Theorie des effizienten Marktes, in der Informationen und die Reaktion darauf in einem starren Kausalzusammenhang stehen, wonach die erhaltenen Informationen unmittelbar reflektiert werden bei Preisen.
Das Konzept des rationalen Anlegers und die Hypothese des effizienten Marktes, basierend auf der Annahme der Beobachtungsunabhängigkeit und der Normalverteilung, wurden erstellt, um probabilistische Berechnungen in der Wirtschaftstheorie anzuwenden. Die Anwendung dieses Konzepts in der Praxis zeigt den Trugschluss dieser vereinfachenden Annahme über einen rationalen Investor, da die objektive Realität die gemachten Berechnungen und Prognosen nicht bestätigt.
Neben der unrealistischen Natur des rationalen Anlegers, mangelnder öffentlicher Verfügbarkeit von Informationen und anormaler Verteilung ignoriert die Kapitalmarkttheorie mit einem linearen Paradigma die Annahme, dass verschiedene Märkte und verschiedene Wertpapiere miteinander verbunden sind.
Im Gegensatz zu linearen Systemen sind nichtlineare dynamische Systeme Systeme, in deren Dynamik:
es gibt eine Rückkopplung, d. h. die Abhängigkeit des gegenwärtigen Geschehens von dem, was in der Vergangenheit passiert ist;
es gibt kritische Niveaus, bei denen mehr als eine Gleichgewichtsposition vorliegt;
dynamische Fraktale werden gebildet;
es besteht eine sensible Abhängigkeit von den Anfangsbedingungen.
All dies deutet darauf hin, dass Finanzmärkte immer noch nichtlineare dynamische Systeme sind und dann folgendes von ihnen erwartet werden kann:
1. Langfristige Korrelationen und Trends, d.h. Rückkopplungseffekte;
2. Variabilität mit kritischen Werten unter bestimmten Bedingungen und zu einem bestimmten Zeitpunkt;
3. Das Vorhandensein einer fraktalen Struktur von Zeitreihen;
4. Abnahme der Prognosesicherheit mit zunehmenden Zeitintervallen, d.h. Manifestationen einer sensiblen Abhängigkeit von den Anfangsbedingungen.
Das obige ist bei Systemen inhärent, die nicht im Gleichgewicht und typisch für die Märkte sind, die wir aus Erfahrung und Praxis kennen.
Effiziente Markttheorie in einem linearen Paradigma ist wie würfelförmige Wolken, die nur in den Köpfen realitätsferner Theoretiker existieren können, deren Wirtschaftsprognosen nie richtig sein werden, weil:
• Anleger sind nicht immer risikoscheu. Sehr oft, fast immer, sind Anleger bereit, Risiken einzugehen, wenn sie erkennen, dass sie ohne Risiko zu Verlusten verdammt sind.
• Die subjektiven Einschätzungen der Anleger sind voller Vorurteile. Sie sind ihren eigenen Vorhersagen viel sicherer, als die verfügbaren Informationen es rechtfertigen.
• Anleger reagieren möglicherweise nicht sofort nach Erhalt auf Informationen. Stattdessen reagieren sie möglicherweise einige Zeit später darauf, wenn sich eine Änderung eines aktuellen Trends bestätigt, was auf eine nichtlineare Reaktion hindeutet.
• Es gibt keine Beweise und keine Beweise dafür, dass Anleger kollektiv als einzeln rational sind.
Die Dominanz des linearen Paradigmas in Bezug auf den Finanzmarkt hört auf, weil die Märkte deutlich gezeigt haben, dass sie in unserem linearen Verständnis selten so geordnet sind, da sehr oft, besonders wenn es am wenigsten erwartet wird, eine exponentielle Superreaktion eintritt auf den Aufprall, was auf Nichtlinearität der Reaktion als auf Linearität hinweist.
Die Chaostheorie und die Wissenschaften nichtlinearer dynamischer Systeme bieten einen anderen Ansatz zur Beschreibung des Geschehens auf dem Finanzmarkt. Um die Vergangenheit zu verstehen, sich der Gegenwart bewusst zu sein und die Zukunft in der Ökonomie zu sehen, ist es notwendig, das lineare Paradigma in ein nichtlineares zu ändern. Die alten Methoden sollten durch neue ersetzt werden, die keine Unabhängigkeit, Rationalität, Random Walks und Normalverteilungen implizieren.
Märkte sollten als nichtlineare dynamische additive synergistische Systeme (NDASS) betrachtet werden und die Wertdynamik sollte durch dynamische Fraktale beschrieben werden. Das nichtlineare Paradigma sollte das Konzept des Langzeitgedächtnisses in die Markttheorie aufnehmen, das postuliert, dass die Ereignisse, die auf den Märkten stattgefunden haben, die Märkte unendlich lange beeinflussen können.
Änderungen in den Notierungen von Finanzinstrumenten, wenn sie nicht in die Wirtschaftstheorie mit einem linearen Paradigma passen, werden in der Regel durch die Auswahl von Nachrichten erklärt, die der Logik entsprechen, und wenn solche Nachrichten nicht gefunden werden können, bleibt alles ohne Erklärung mit die Hoffnung auf zukünftige Nachrichten, die in die Logik des Geschehenen passen.
Im Gegensatz zum linearen Paradigma gibt das nichtlineare Paradigma immer eine Antwort auf die Frage nach den Gründen für die eine oder andere Preisdynamik am Finanzmarkt, unabhängig vom Finanzinstrument und dem Markt, auf dem es gehandelt wird.
Es ist an der Zeit, mit dem linearen Paradigma aufzuhören und auf die Schienen eines nichtlinearen Paradigmas überzugehen, das die Möglichkeit bietet, die Wertdynamik des Finanzmarktes zu modellieren.
3. Methode zur Modellierung der Wertdynamik am Finanzmarkt.
3.1. Vorwort. Bevor wir direkt zur Betrachtung der Methode zur Modellierung der Wertdynamik am Finanzmarkt übergehen, sei eine kurze Einführung gegeben. Die Theorie der nichtlinearen dynamischen Systeme wurde entwickelt, um die Bewegung von Teilchenströmen in physikalischen Medien wie Gas, Flüssigkeit, Plasma zu beschreiben. Wenn sich die Größe äußerer Einflüsse auf das System, beispielsweise Temperatur oder Druck, ändert, ermöglicht die Theorie es, die Dynamik von Strömungen in diesen Medien entsprechend den Parametern der äußeren Einflüsse zu beschreiben und zu simulieren. Wenn der Finanzmarkt die Eigenschaften eines nichtlinearen dynamischen Systems besitzt, stellt sich eine völlig logische Frage – lässt sich die Theorie der nichtlinearen dynamischen Systeme auf die Beschreibung und Modellierung der Dynamik des Finanzmarktes anwenden? Die Antwort lautet: Ja, das können Sie! Erinnern wir uns an die Definition des Begriffs "Finanzen". Finanzen ist eine Reihe von wirtschaftlichen Beziehungen, die im Prozess der Bildung, Verteilung und Verwendung von zentralen und dezentralen Dachfonds entstehen. Aus der Definition folgt, dass Finanzen Cashflows sind, dh Finanzen sind Dynamiken. Ein Wirtschaftssystem ist analog zu einem physikalischen System, und es gibt hier und da Partikelströme. In einem physikalischen System können solche Partikel Gas-, Wasser- oder Plasmapartikel sein, und in einem wirtschaftlichen System können solche Partikel in all ihren Formen und Erscheinungsformen als Geld angesehen werden. Ein äußerer Einfluss auf ein physikalisches System, beispielsweise eine Änderung von Parametern wie Temperatur, Druck oder beidem, führt zu einer Änderung der Strömungsdynamik in diesem System. Ebenso können wir von einem Wirtschaftssystem sprechen, in dem sich unter äußeren Einflüssen, wie z. B. einer Änderung des Zinssatzes, von Angebot und Nachfrage, der Profitrate in einer Branche usw Cashflows, die ihre Richtung sowohl innerhalb des lokalen Marktes als auch zwischen verschiedenen anderen Märkten ändern - Devisen, Aktien, Rohstoffe, Rohstoffe, dh innerhalb des allumfassenden Finanzmarktes. Finanzmärkte stellen Cashflows in der Wirtschaft dar, und diese Cashflows sind nicht einheitlich, sie können in Analogie zu den in verschiedenen physischen Systemen erzeugten Strömen als turbulent und chaotisch charakterisiert werden. Der Generator des einfachsten Cashflows ist ein Mensch als Subjekt von Wirtschaftsbeziehungen, der von seiner Umwelt, einschließlich des Informationsfeldes, beeinflusst wird. Jeder Mensch verfügt über einen bestimmten Geldbetrag, der ihm in Form von Gehältern, Sozialleistungen, Dividenden, Zinsen und anderen Einkünften aus nicht aufzählbaren Quellen zukommt. Wenn eine Person ihr Geld ausgibt, ohne es zu merken, generiert sie bestimmte Cashflows. Diese Cashflows von Menschen einzeln sind kaum wahrnehmbar und nicht wahrnehmbar, sie sind wie Wassertropfen, aus denen geformte dünne Bäche in Bäche ergießen, dann mit Bächen in Flüsse, von Flüssen zu Meeren und weiter in Ozeane, gefolgt von Verdunstung und wieder Umwandlungen in Tropfen. Cashflows, die von Hunderten, Tausenden, Millionen Menschen generiert werden, werden bereits sichtbar und greifbar. Zum Beispiel hat die Nachfrage nach Apple-Produkten enorme Cashflows generiert, die es geschafft haben, die Marktkapitalisierung des Unternehmens dramatisch zu erhöhen. Im Allgemeinen ist der Finanzmarkt ein nichtlineares dynamisches System mit ungleichmäßigen Cashflows, was bedeutet, dass Sie zur Beschreibung der Dynamik des Finanzmarktes alle Werkzeuge verwenden können, die nur auf nichtlineare dynamische Systeme anwendbar sind. In physikalischen Systemen ist die Zahl der äußeren Einflüsse eine endliche Zahl. Wenn wir in der Sprache der Mathematik sprechen, dann wird ein äußerer Einfluss als eine bestimmte Größe verstanden. Bei endlich vielen Variablen kann man das Konzept einer Funktion einführen, die die Abhängigkeit der Strömungsdynamik von Änderungen dieser Variablen beschreibt, und die Abhängigkeit selbst kann durch eine Gleichung mit endlich vielen Lösungen ausgedrückt werden. Beispielsweise ermöglicht das Vorhandensein von zwei äußeren Einflüssen in Form von Temperatur und Druck in einem physikalischen System, die Strömungsänderungsgeschwindigkeit als Funktion dieser beiden Größen darzustellen. Aber ein Wirtschaftssystem ist weit davon entfernt, ein physikalisches System zu sein, in dem man unendlich oft experimentieren, die Parameter äußerer Einflüsse ändern und dieses System schließlich wieder in seinen ursprünglichen Zustand zurückversetzen kann. Der Finanzmarkt ist ein System, das keine endliche Anzahl externer Einflüsse hat. Alles, vom Diskontsatz bis hin zu unbestätigten Gerüchten, kann externe Einflüsse sein. Wir können sagen, dass der Wert auf dem Finanzmarkt eine Funktion einer unendlichen Anzahl externer Einflüsse ist, die unabhängige Variablen sind: P = F (x1, x2, x3, …, xn) wo P ist der Preis eines finanziellen Vermögenswerts; Xn ist äußerer Einfluss, n → ∞. Die Lösung dieser Gleichung, d.h. Den Wert des zukünftigen Wertes eines finanziellen Vermögenswerts zu ermitteln, ist bei dieser Problemstellung nicht möglich. Ein anderer Ansatz ist erforderlich. Denken Sie daran, dass die Lösung einer quadratischen Gleichung nicht nur durch Formeln aus der Gleichung einer Funktion gefunden werden kann, sondern auch durch den Graphen dieser Funktion. Der Ansatz, bei dem die Lösung einer Gleichung grafisch gefunden werden kann, ist auf nichtlineare dynamische Systeme anwendbar. Dazu werden wir mehrere Annahmen treffen. Cashflows werden in Werten ausgedrückt. Die Dynamik der Cashflows zwischen Wirtschaftseinheiten spiegelt sich also in den Jahresabschlüssen dieser Unternehmen wider, jedoch auf globaler Ebene - in den Handelsbilanzen der Länder. Die Dynamik der Cashflows auf dem Finanzmarkt spiegelt sich in der Dynamik des Wertes von Finanzanlagen wider. Organisierte Märkte (Börsen, elektronische Handelsplattformen) in Verbindung mit Informationstechnologien geben uns die einzigartige Möglichkeit in Echtzeit die Dynamik der Cashflows auf den Devisen-, Aktien-, Rohstoff- und Rohstoffmärkten sowohl in einer bestimmten Region als auch in in der globalen Welt. Betrachten wir den Mechanismus der Preisbildung von Finanzinstrumenten auf dem organisierten Markt. Anleger, die etwas kaufen oder verkaufen möchten, platzieren entsprechende Aufträge zum Kauf oder Verkauf bestimmter finanzieller Vermögenswerte. Die zum Kauf zu einem bestimmten Preis aufgegebenen Ordermengen, die die zum gleichen Preis zum Verkauf angebotenen Ordermengen übersteigen, führen zu einem bestimmten Zeitpunkt zu einer Preissteigerung dieses finanziellen Vermögenswerts. Umgekehrt führt das Volumen der zum Verkauf angebotenen Aufträge zu einem bestimmten Preis, das das Volumen der zum gleichen Preis zum Kauf angebotenen Aufträge übersteigt, zu einem bestimmten Zeitpunkt zu einer Senkung des Preises des finanziellen Vermögenswerts. Somit kann man sagen, dass nur ein einziger Faktor den Preis eines finanziellen Vermögenswerts beeinflusst, nämlich die Orders der Anleger im Orderbuch. Nur platzierte und ausgeführte Orders bewegen die Preise nach unten oder nach oben. In diesem Fall können alle organisierten Märkte, die alle am Prozess Beteiligten einbeziehen – von Regulierungsbehörden und Organisatoren von Geschäften bis hin zu Käufern und Verkäufern, auf denen Finanzinstrumente gehandelt werden, konventionell als eine Art Blackbox betrachtet werden, an deren Ausgang durch ein glas, als eine art messgerät werden zitate zu jedem bestimmten zeitpunkt abgelesen. Die im Chart eingezeichneten Messwerte aus dem Orderbuch beschreiben die Dynamik der Cashflows. Um alles so weit wie möglich zu vereinfachen, kann der Graph der Kostenänderung im Laufe der Zeit als Graph der Funktion N dargestellt werden, die ein Operator ist, der die Übereinstimmung zwischen der Menge von Werten von P und der Menge von Werten festlegt von T: P = N (T) wo P ist der Preis eines finanziellen Vermögenswerts; T ist Zeit. Unter Berücksichtigung der Tatsache, dass dies ein Graph einer nichtlinearen Funktion ist, der die Dynamik eines nichtlinearen dynamischen Systems beschreibt, können wir sagen, dass der Graph ein Attraktor ist, dessen Struktur durch dynamische Fraktale gebildet wird. Um fortzufahren, müssen Sie einige Konzepte und ihre Definitionen auffrischen. Dynamisches System. Ein dynamisches System wird als ein Prozess verstanden, für den das Konzept eines Zustands eindeutig als eine Menge von Werten einiger Größen zu einem bestimmten Zeitpunkt definiert ist und ein Operator angegeben ist, der die Entwicklung des Anfangszustands in der Zeit bestimmt. Attraktor. Attractor (engl. anziehen - anziehen, anziehen) ist eine kompakte Teilmenge des Phasenraums eines dynamischen Systems, dessen Trajektorien aus irgendeiner Umgebung dazu tendieren, zur Zeit ins Unendliche zu streben. Ein Attraktor kann eine periodische Trajektorie oder ein begrenzter Bereich mit instabilen Trajektorien im Inneren im Fall eines seltsamen Attraktors sein. Ein seltsamer Attraktor. Die Besonderheit eines seltsamen Attraktors liegt in seiner Skaleninvarianz, die sich darin ausdrückt, dass bei Vergrößerung oder Verkleinerung der Skala einer bestimmten Unterdomäne eines seltsamen Attraktors ein geometrisches Objekt erhalten wird, das in seiner Struktur dem gesamten Attraktor ähnlich ist. Phasenraum. Der Phasenraum eines Systems ist eine Sammlung aller zulässigen Zustände eines dynamischen Systems. Somit ist ein dynamisches System durch seinen Anfangszustand und das Gesetz charakterisiert, nach dem das System von einem Zustand in einen anderen übergeht. Verzweigungspunkt. Ein Bifurkationspunkt ist ein kritischer Zustand eines dynamischen Systems, bei dem das System gegenüber in ihm auftretenden Fluktuationen instabil wird und Unsicherheit entsteht: Bleibt der Zustand des Systems chaotisch oder bewegt es sich auf eine neue, höhere Ordnungsebene. Chaos. Chaos ist eine sich nicht wiederholende, unregelmäßige, ungeordnete Folge von Zuständen eines dynamischen Systems oder das ungeordnete Verhalten der Attraktoren dieses Systems. Fraktal. Ein Fraktal ist eine Struktur, die aus Teilen besteht, die einem Ganzen ähnlich sind. Man kann auch sagen, dass ein Fraktal ein Attraktor eines nichtlinearen dynamischen Systems ist. Dynamisches Fraktal. Dynamische Fraktale beschreiben die Dynamik von zeitlichen Prozessen in nichtlinearen dynamischen Systemen. Ein nichtlineares dynamisches System durchläuft in seiner Entwicklung alternierende Stadien eines stabilen und chaotischen Zustands, wodurch aus dem Chaos geordnete Zustände entstehen, die das System wieder in einen chaotischen Zustand bringen. Synergien. Synergetik (von griech. synergeia - Kooperation, Hilfe, Komplizenschaft) ist eine interdisziplinäre Richtung wissenschaftlicher Forschung, in deren Rahmen die allgemeinen Gesetzmäßigkeiten der Übergangsprozesse vom Chaos in die Ordnung und zurück (Prozesse der Selbstorganisation und spontanen Desorganisation) in offenen nichtlinearen Systemen physikalischer, chemischer, biologischer, ökologischer, sozialer und anderer Natur. Das Wesen des synergetischen Ansatzes zur Beschreibung der Dynamik des Finanzmarktes besteht darin, dass komplexe Systeme, die aus einer Vielzahl von Elementen in komplexen Interaktionen miteinander bestehen und eine Vielzahl von Freiheitsgraden besitzen, durch wenige wesentliche Typen beschrieben werden können der Bewegung (Ordnungsparameter) und alle anderen Bewegungsarten erweisen sich als untergeordnet und können ziemlich genau in den Ordnungsparametern ausgedrückt werden. Daher kann das komplexe Verhalten von Systemen wie dem Finanzmarkt durch eine Hierarchie vereinfachter Modelle beschrieben werden, die eine kleine Anzahl der wichtigsten Freiheitsgrade umfassen.
3.2. Der Finanzmarkt ist die NDASS.
Der Finanzmarkt ist ein nichtlineares dynamisches System. Es ist das nichtlineare Paradigma, das es ermöglicht, die Dynamik des Finanzmarktes mit den geeigneten mathematischen Werkzeugen für nichtlineare dynamische additive synergetische Systeme (NDASS) zu verstehen und zu beschreiben.
Die Methode zur Modellierung der Dynamik von Notierungen von Finanzinstrumenten basiert auf:
- Chaostheorie;
- fraktale Geometrie;
- Synergetik.
3.3. Die Kosten sind eine Funktion der Zeit: P = N (T).
Basierend auf der Tatsache, dass der Finanzmarkt ein nichtlineares dynamisches System ist, kann der Graph der Wertänderung eines finanziellen Vermögenswerts von Zeit zu Zeit als Graph der Funktion N angesehen werden, bei der es sich um einen Operator handelt, der die Korrespondenz zwischen festlegt die Menge der P-Werte und die Menge der T-Werte: P = N(T) wo P – Preis eines finanziellen Vermögenswerts; T – Zeit. Unter Berücksichtigung der Tatsache, dass dies ein Graph einer nichtlinearen Funktion ist, die die Dynamik eines nichtlinearen dynamischen Systems beschreibt, können wir sagen, dass dieser Graph ein Attraktor ist, dessen Struktur durch dynamische Fraktale gebildet wird.
3.4. Fraktale und fraktale Struktur.
Die Methode zur Modellierung der Wertdynamik eines finanziellen Vermögenswerts basiert auf der Analyse des Attraktors des Operators N, der seine fraktale Struktur bildet, was ein Verständnis dafür vermittelt, welche Fraktale gebildet wurden, welche Fraktale gebildet werden und als Ergebnis, welche Fraktale gebildet werden, wodurch die zukünftigen Richtungen der möglichen Dynamik seines Wertes gezeigt werden.
Lassen Sie uns die Definition von Fraktal und Fraktalstruktur einführen.
Mit fraktal ist der einfachste Attraktor der Oszillationsbewegung gemeint, der aus drei Segmenten besteht, von denen eines (2. Segment) in die entgegengesetzte Richtung zu den beiden anderen (1. und 3. Segment) gerichtet ist.
Fraktale werden abhängig von der Größe der Kosten und den Zeitintervallen ihrer Segmente in Typen und Typen unterteilt.
Gemäß der Eigenschaft der Selbstähnlichkeit bilden Fraktale niedrigerer Ordnung Fraktale höherer Ordnung, dementsprechend bestehen Fraktale höherer Ordnung aus Fraktalen niedrigerer Ordnung.
3.5. Die Reihenfolge, Arten und Typen von Fraktalen.
Somit weist jedes Fraktal zusätzlich zu den Kosten- und Zeitwerten der Intervalle die folgenden Merkmale auf, die es beschreiben:
1. Die Reihenfolge eines Fraktals, die angibt, um welches Segment es sich in Bezug auf Fraktale höherer Ordnung handelt und welche Segmente von Fraktalen niedrigerer Ordnung es selbst bildet.
2. Die Art des Fraktals.
3. Ansicht des Fraktals.
Fraktale Struktur ist in diesem Fall die Verbindung von Fraktalen verschiedener Ordnungen, Typen, Typen untereinander.
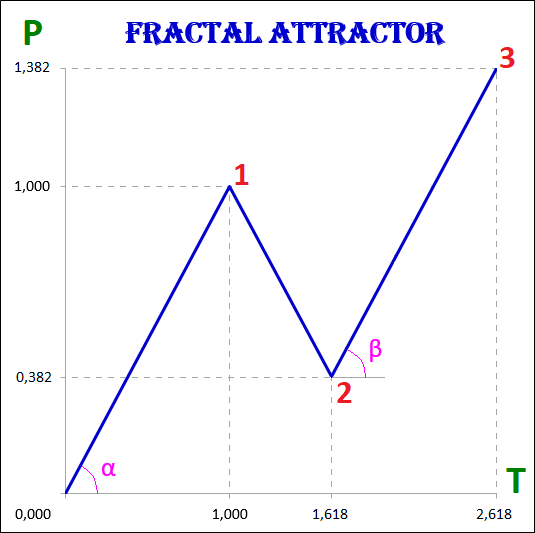
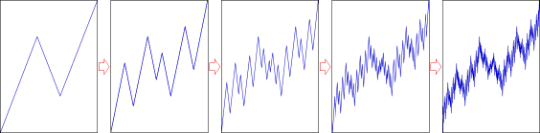
3.8. Grundlegende fraktale Dynamik.
In diesem Beispiel haben alle Segmente von Fraktalen - sowohl das erste als auch das zweite und das dritte, unabhängig von ihrer Reihenfolge - das erste, zweite, dritte, vierte oder fünfte die Kosten- und Zeitintervalle des grundlegenden fraktalen Attraktors, nämlich: 1) P1 = P3 und T1 = T3; 2) P2 / P1 = T2 / T1 = 0,618.
3.9. Beschreibung der fraktalen Struktur.
Die tatsächliche Marktdynamik des Werts eines finanziellen Vermögenswerts wird vom Betreiber N beschrieben.
Ein grundlegendes Fraktal ist eines der vielen Fraktale, die die fraktale Struktur der Graphen der Wertedynamik bilden, die Attraktoren sind.
Die fraktale Struktur eines Attraktors zu beschreiben bedeutet, die Arten und Typen von Fraktalen seiner Komponenten, ihre Reihenfolge und Position in Bezug zueinander zu beschreiben.
Die fraktale Struktur des Attraktors ist sowohl so komplex als auch so einfach, dass es unmöglich ist zu sagen, was mehr in der Tabelle der Notierungen von finanziellen Vermögenswerten steht - Chaos oder Ordnung.
Zuerst werden wir eine Definition von Chaos und Ordnung in einer fraktalen Struktur geben, dann werden wir die Bezeichnung von Fraktalen in einer fraktalen Struktur beschreiben, wonach wir ihre Klassifizierung nach Typen und Typen geben werden.
3.10. Bestimmung von Ordnung und Chaos.
Ordnung ist ein komplettes Fraktal. Ein Fraktal gilt als abgeschlossen, wenn alle drei Segmente gebildet sind - das 1., 2. und 3.. Die Fertigstellung des 3. Segments zeigt die Fertigstellung des gesamten Fraktals an, da der sequentiellen Fertigstellung des 1. und 2. Segments vorausgeht. Chaos ist in diesem Fall der Prozess der fraktalen Bildung.
Mit anderen Worten, die Ordnung ist diskret und das Chaos ist kontinuierlich. Die Vervollständigung des 3. Segments eines Fraktals wird durch den Beginn des 1. Segments eines anderen Fraktals derselben Ordnung oder höher ersetzt.
Unter Berücksichtigung der Tatsache, dass Fraktale niedrigerer Ordnung Fraktale höherer Ordnung bilden, können wir sagen, dass Chaos und Ordnung untrennbar miteinander verbunden sind.
Ordnung ist im Chaos vorhanden und Chaos ist in Ordnung vorhanden. Chaos und Ordnung durchdringen sich gegenseitig und existieren ineinander.
Die Wertdynamik am Finanzmarkt kann sowohl als chaotisch als auch als geordnet bezeichnet werden. Das Chaos selbst ist jedoch nichts anderes als eine Ordnung auf höchstem Niveau, da nichts Chaotisches passiert, da der Graph dieser Dynamik ein Attraktor eines vom Operator N bestimmten dynamischen Fraktals ist.
3.11. Die Reihenfolge der Fraktale.
Jedes Fraktal ist das erste, zweite oder dritte Segment eines anderen Fraktals, das eine höhere Ordnung hat.
Für eine genaue Beschreibung der Position von Fraktalen in einer Fraktalstruktur ist ihre Bezeichnung erforderlich, die Zuordnung bestimmter Zahlen zu den Fraktalen, wodurch eindeutig verstanden werden kann, welche Segmente Fraktale sind und in welcher Reihenfolge sie in Bezug auf andere Fraktale angeordnet sind.
Ein Fraktal, dessen Nummer aus einer Ziffer besteht, ist das höchste Fraktal 1. Ordnung.
Ein Fraktal, dessen Nummer aus zwei Ziffern besteht, ist ein Fraktal 2. Ordnung, von drei - von 3. Ordnung, von vier - von 4. usw.
Fraktale 4. Ordnung bilden die Fraktale 3. Ordnung, die wiederum die Fraktale 2. Ordnung bilden, und diese bilden bereits die Fraktale höchster 1. Ordnung.
3.12. Nummerierung von Fraktalen.
Das Fraktal höchster Ordnung 1. Ordnung wird mit 1, 2 oder 3 nummeriert, je nachdem, ob es sich um das erste, zweite oder dritte Segment handelt. Ein Fraktal 1. Ordnung besteht aus Segmenten, die Fraktale 2. Ordnung sind. Fraktale Nummer 1 besteht aus Segmenten mit den Nummern 11 (1. Segment), 12 (2. Segment) und 13 (3. Segment). Das Fraktal mit der Nummer 2 besteht aus den Segmenten 21 (1. Segment), 22 (2. Segment) und 23 (3. Segment). Fraktale Nummer 3 besteht aus Segmenten mit den Nummern 31 (1. Segment), 32 (2. Segment) und 33 (3. Segment). Fraktale haben dieselbe Reihenfolge, wenn sie entweder Segmente eines Fraktals sind, aus dem es besteht, oder Segmente anderer Fraktale, die wiederum Segmente eines anderen Fraktals sind. Ein Fraktal ist eine Größenordnung kleiner als ein anderes Fraktal, wenn es ein Segment davon ist. Ein Fraktal ist eine Größenordnung größer als ein anderes Fraktal, wenn dieses andere Fraktal ein Segment davon ist. Ein durch eine Zahl angegebenes Fraktal ähnelt einem durch Koordinaten angezeigten Punkt, der im entsprechenden Koordinatensystem leicht zu finden ist. In unserem Fall ist das Koordinatensystem eine fraktale Struktur. Wenn zum Beispiel die Koordinaten des Fraktals die Nummer 132 sind, bedeutet dies, dass dieses Fraktal das 2. Segment des Fraktals 2. Ordnung mit der Nummer 13 ist, das wiederum das 3. Segment des Fraktals 1. Ordnung mit der Nummer ist 1.
3.13. Bestimmung von Extremumpunkten.
Die Wertdynamik am Finanzmarkt ist eine Abwechslung von Aufwärtstrends und Abwärtstrends mit der Bildung lokaler und globaler Extrempunkte in den Charts.
Unter dem Gesichtspunkt der fraktalen Struktur von Diagrammen sind Extrempunkte (Punkte, an denen sich Trends ändern) Punkte, an denen einige fraktale Segmente ihre Bildung abschließen und andere beginnen, sich zu bilden.
3.14. Arten und Typen von Fraktalen.
Das Fraktal besteht aus drei Segmenten - dem ersten, dem zweiten und dem dritten. Das zweite Segment des Fraktals ist immer in die entgegengesetzte Richtung zum ersten und dritten Segment gerichtet. Zusätzlich zu der Reihenfolge, in der auch die Segmentnummer angegeben ist, weist jedes fraktale Segment zwei Merkmale (zwei Parameter) auf - den Preis P (Kostenintervall) und die Zeit T (Zeitintervall). P ist ein Wertmerkmal, das die Länge der Projektion eines fraktalen Segments auf die Preisachse zeigt und damit das Preisintervall angibt, in dem das Segment gebildet wurde. T ist eine zeitliche Charakteristik, die die Länge der Projektion des fraktalen Segments auf die Zeitachse zeigt, wodurch das Zeitintervall angegeben wird, das zur Bildung des Segments benötigt wurde. Ein aus drei Segmenten bestehendes Fraktal weist sechs Merkmale auf: P1, P2, P3, T1, T2, T3: • P1 und T1 - Preis- und Zeitintervalle des 1. Segments; • P2 und T2 - Preis- und Zeitintervalle des 2. Segments; • P3 und T3 - Preis- und Zeitintervalle des 3. Segments. Das Hauptfraktal ist ein Grundfraktal, dessen Kosten- und Zeitparameter der Segmente in folgenden Anteilen miteinander in Beziehung stehen: 1. Anteil: P1/P3 = T1/T3 = 1; 2. Anteil: P2/P1 = T2/T1 = 0,618. Durch Ändern der Werte der Parameter des Basisfraktals unter Verwendung der Fibonacci-Koeffizienten unter Verwendung des goldenen Schnitts erhalten wir eine Reihe von Fraktalen, die nach Ansichten und Typen klassifiziert werden können. Drei Arten von Fraktalen können vom Verhältnis der Kostenparameter des 1. und 3. Segments unterschieden werden. Ansicht Nr. 1 - Dies sind Fraktale, bei denen das Preisintervall des dritten Segments größer ist als das Preisintervall des ersten Segments: P1 < P3; Ansicht Nr. 2 - Dies sind Fraktale, bei denen das Preisintervall des dritten Segments dem Preisintervall des ersten Segments entspricht: P1 = P3; Ansicht Nr. 3 - Dies sind Fraktale, bei denen die Preisspanne des dritten Segments geringer ist als die Preisspanne des ersten Segments: P1 > P3. In Bezug auf jede Art von Fraktalen können wir sagen, dass die zweite Art von Fraktalen die normale Dynamik charakterisiert, die erste Art von Fraktalen die Dynamik mit Beschleunigung charakterisiert und die dritte Art von Fraktalen die Dynamik mit Verzögerung charakterisiert. Aus den Verhältnissen der Kosten- und Zeitparameter des 1., 2. und 3. Segments können in jeder Form fünf Typen von Fraktalen unterschieden werden. Drei Arten und fünf Typen ergeben 15 Fraktale, einschließlich des Basistyps. Fraktale des 1. Arten sind mit folgenden Zahlen gekennzeichnet: 11, 12, 13, 14, 15. Fraktale des 2. Arten sind mit folgenden Zahlen gekennzeichnet: 21, 22, 23, 24, 25. Fraktale des 3. Arten sind mit folgenden Zahlen gekennzeichnet: 31, 32, 33, 34, 35. Die erste Ziffer in der Nummer gibt die Art des Fraktals an - 1., 2. oder 3., und die zweite Ziffer in der Nummer gibt die Typ des Fraktals an - 1., 2., 3., 4. oder 5..
Betrachten wir jedes der 15 Fraktale separat und bezeichnen die Proportionen zwischen den Werten der Kosten- und Zeitintervalle seiner konstituierenden Segmente.
Beginnen wir mit den Fraktalen des 1. Art, fahren wir mit den Fraktalen des 2. Art fort und enden mit den Fraktalen des 3. Art.
3.15. 15 Fraktale:
3.15.1. Fraktale des 1. Art.
Fraktale des 1. Typs haben folgende Zahlen: 11, 12, 13, 14, 15.
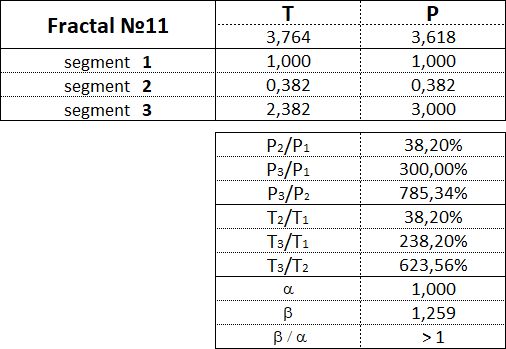
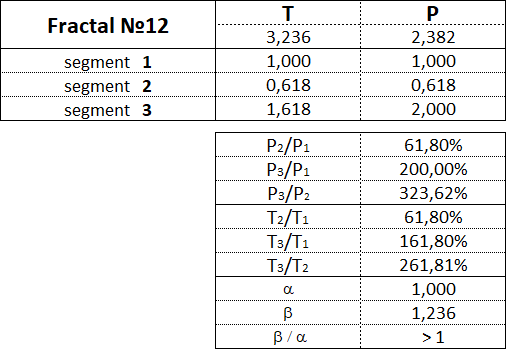
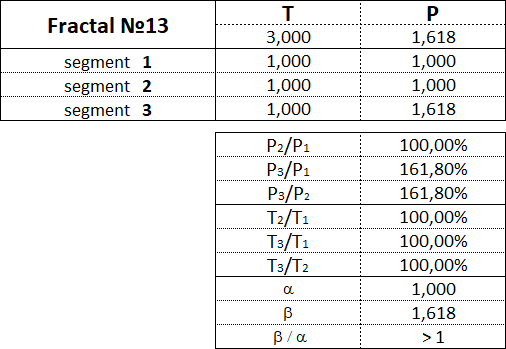
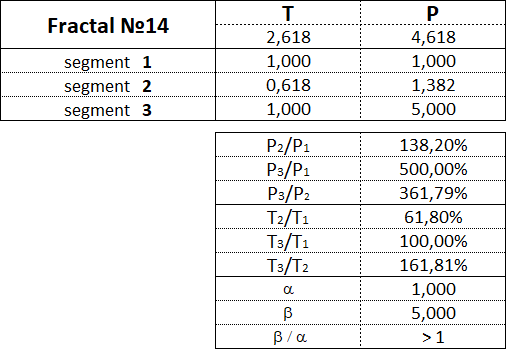
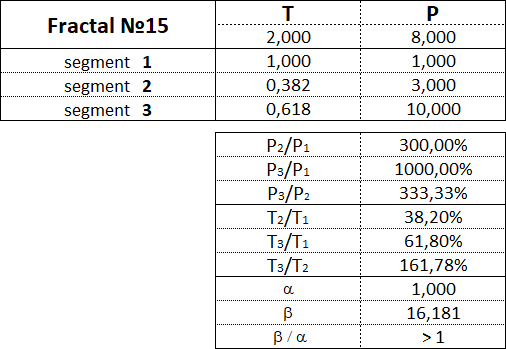
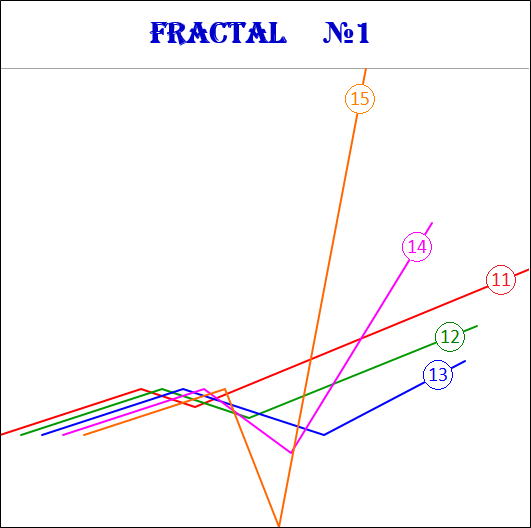
3.15.2. Fraktale des 2. Art.
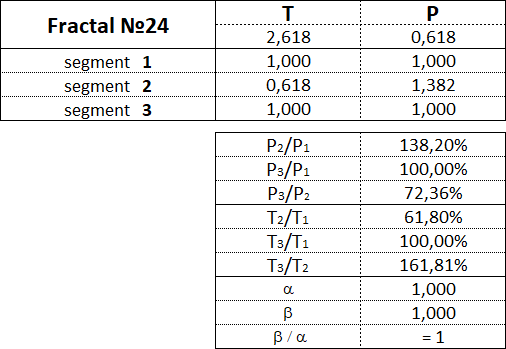
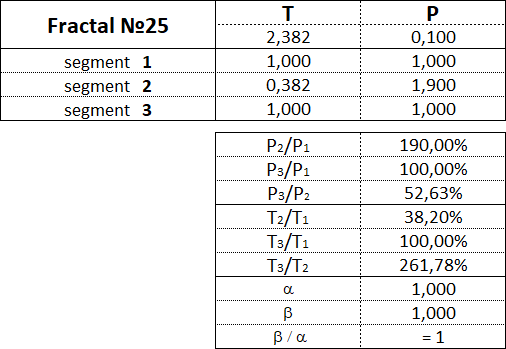
Fraktale des 2. Art haben folgende Zahlen: 21, 22, 23, 24, 25.
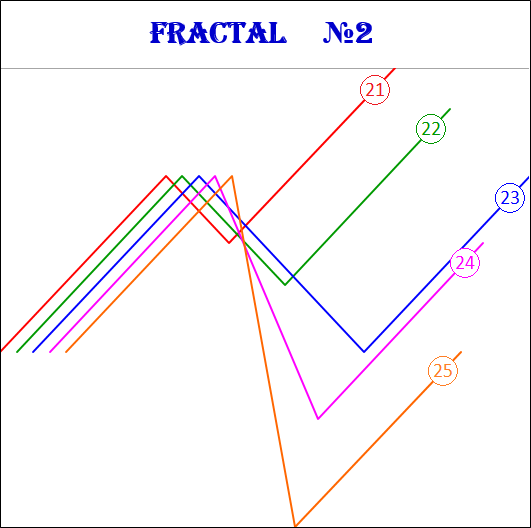
3.15.3. Fraktale des 3. Art.
Fraktale des 3. Art haben folgende Zahlen: 31, 32, 33, 34, 35.
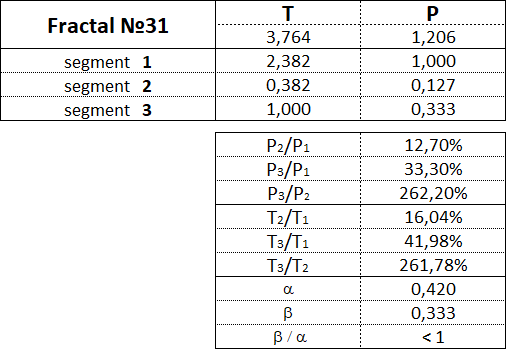
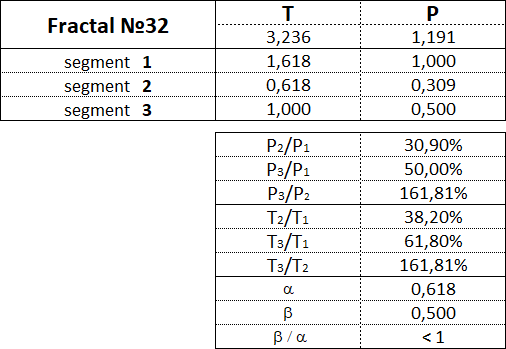
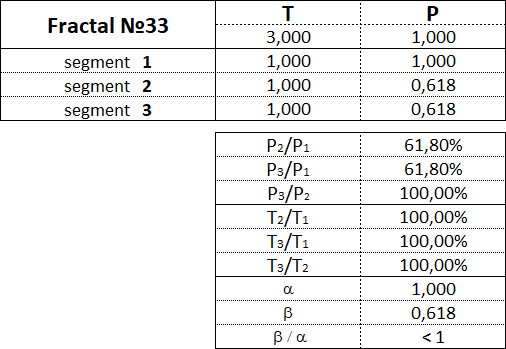
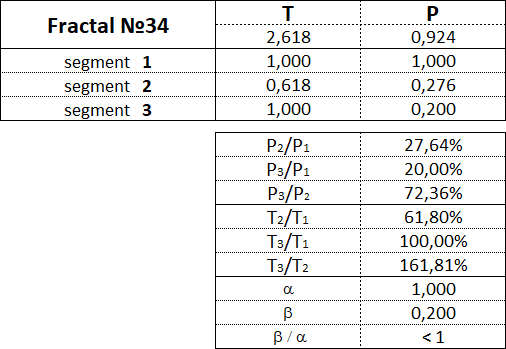
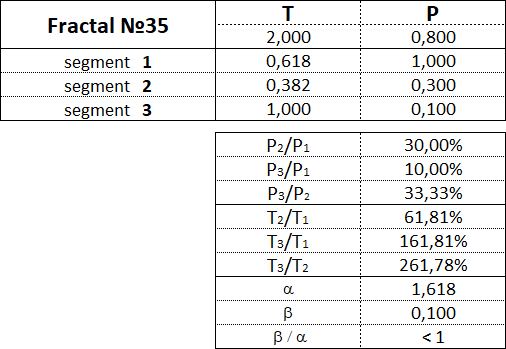
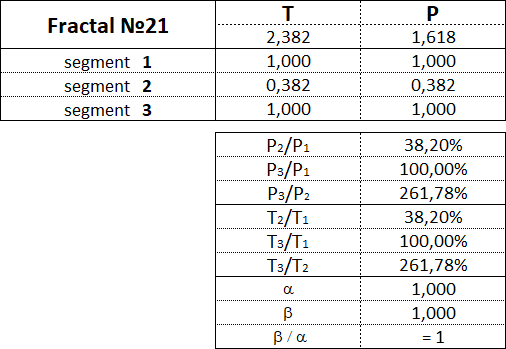
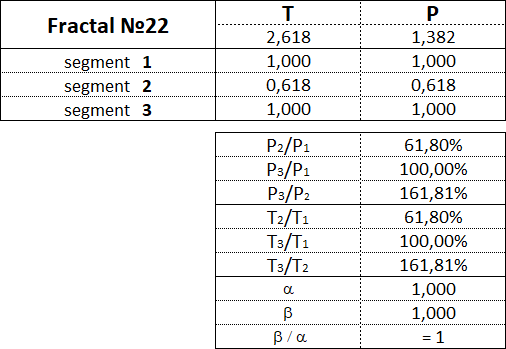
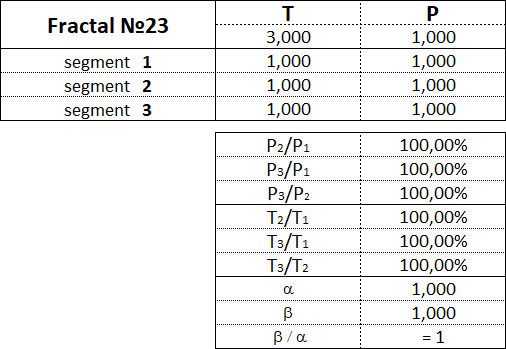
3.16. Proportionen zwischen fraktalen Segmenten.
Diese Tabelle zeigt die Wertebereiche als Prozentsatz zwischen den Kosten- und Zeitparametern der Segmente für jedes der 15 Fraktale.
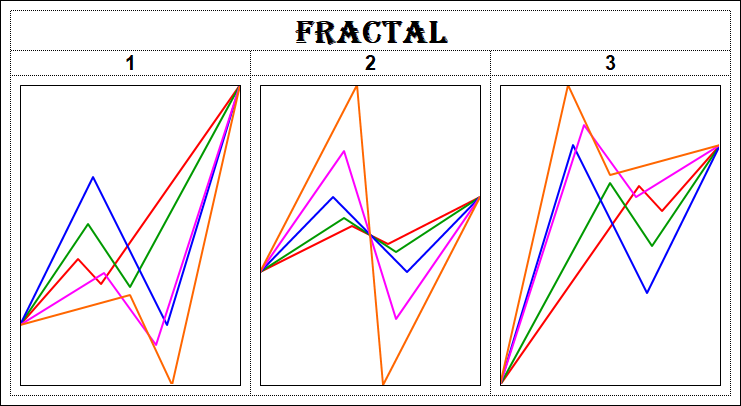
3.17. Das Alphabet der Niro-Attraktoren.
Aus 15 Fraktalen kann man sich eine Art Alphabet aus 15 Buchstaben zusammenstellen.
Wie im Morsecode können Sie mit Kombinationen aus zwei Symbolen - Punkten und Strichen - jeden beliebigen Text schreiben, und im Alphabet der Attraktoren Niro können Kombinationen von 15 Fraktalen jede fraktale Struktur FS eines beliebigen Basic Anlagegut BA beschreiben.
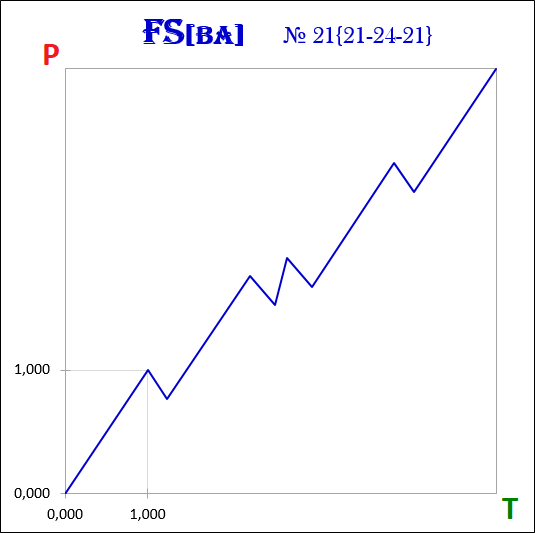
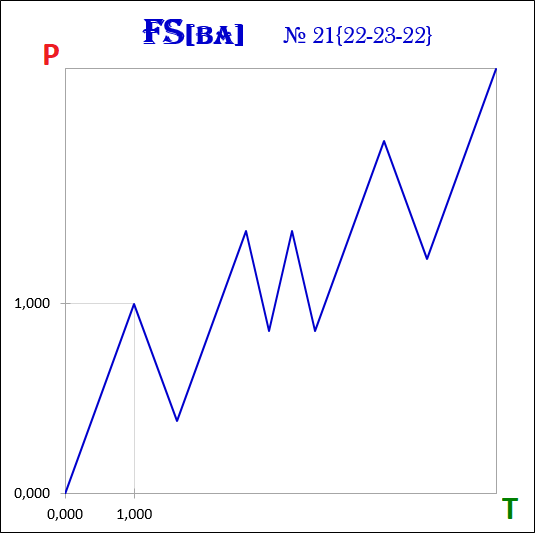
3.18. Verzweigungspunkt und Freiheitsgrade.
Ein nichtlineares dynamisches System bleibt im Chaos, bis ein Fraktal in der fraktalen Struktur des Diagramms gebildet wird. Ein gebildetes Fraktal bedeutet, dass das System von einem chaotischen Zustand in einen geordneten Zustand übergegangen ist. Die aus dem Chaos entstandene Ordnung wird durch den Beginn der Bildung eines neuen Fraktales in entgegengesetzter Richtung zum bereits gebildeten gestört, und das System wird in einen chaotischen Zustand zurückkehren.
Im Moment der Vervollständigung des Fraktales befindet sich ein nichtlineares dynamisches System an einem Verzweigungspunkt, an dem das System mehrere Freiheitsgrade besitzt – mehrere Optionen für die Weiterentwicklung seiner fraktalen Struktur. Am Bifurkationspunkt kann eindeutig nur von einem Trendwechsel gesprochen werden, also einem Richtungswechsel des zukünftigen Fraktals in das Gegenteil des fertigen Fraktals, alles andere – die Kosten und Zeitintervalle zukünftiger Fraktale, bleibt unklar, nicht eindeutig definierbar.
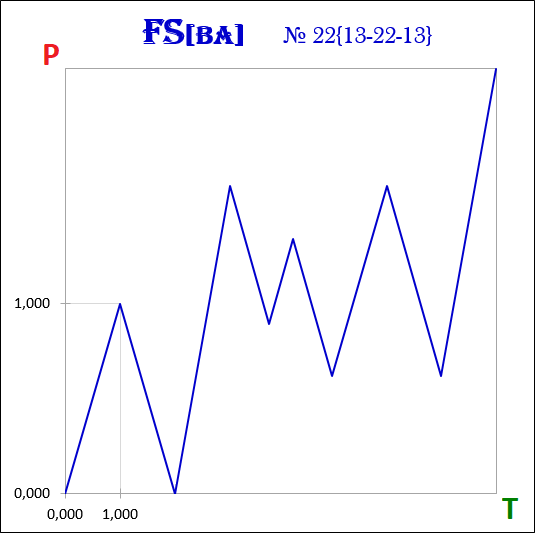
Betrachten wir ein Beispiel für die Bildung einer fraktalen Struktur eines nichtlinearen dynamischen Systems mit zwei Freiheitsgraden an Verzweigungspunkten für drei Zeitintervalle. Unter Zeitintervall wird die Zeitspanne verstanden, die für die Bildung von Fraktalen gleicher Ordnung notwendig ist.
Entwicklungsszenario 1 ist ein Szenario, bei dem das Kostenintervall eines neuen Fraktals das Kostenintervall des fertigen Fraktals nicht überschreitet.
Das zweite Entwicklungsszenario ist ein Szenario, bei dem das Kostenintervall des neuen Fraktals das Kostenintervall des abgeschlossenen Fraktals überschreitet.
Bezeichnen wir mit T0 das Zeitintervall, für das das anfängliche Fraktal gebildet wurde.
Dann können im T1-Intervall zwei Fraktale gebildet werden, im T2-Intervall - vier Fraktale und im T3-Intervall - acht Fraktale.
Die Anzahl der Freiheitsgrade an Verzweigungspunkten eines nichtlinearen dynamischen Systems bestimmt die Anzahl der möglichen Szenarien für die Entwicklung seiner fraktalen Struktur im aktuellen Zeitintervall, die mit jedem weiteren Zeitintervall exponentiell ansteigen.
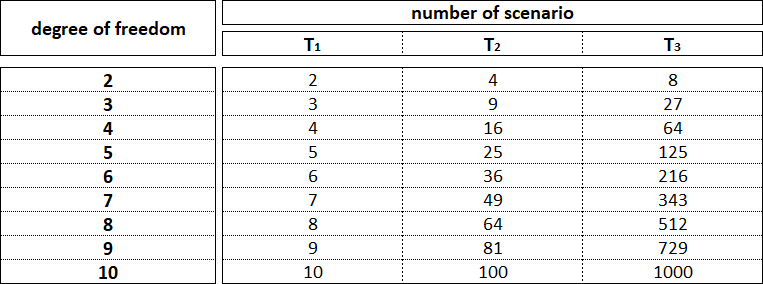
Die Anzahl der Freiheitsgrade am Verzweigungspunkt eines nichtlinearen dynamischen Systems ist nicht konstant und hängt von seiner Lage in der fraktalen Struktur ab.
Ein nichtlineares dynamisches System hat die minimale Anzahl an Freiheitsgraden, wenn der Verzweigungspunkt in der fraktalen Struktur am Beginn der Bildung des Fraktals kleinster Ordnung liegt, das das Fraktal größter Ordnung vervollständigt.
Die maximale Anzahl von Freiheitsgraden fällt auf den Verzweigungspunkt, der den Abschluss des Fraktals höchster Ordnung und den Beginn des Fraktals niedrigster Ordnung trennt.
Vor diesem Hintergrund hat die Modellierung der fraktalen Struktur eines nichtlinearen dynamischen Systems über das zweite Zeitintervall hinaus aufgrund der Vielzahl möglicher Szenarien für die Entwicklung einer fraktalen Struktur keine praktische Bedeutung.
3.19. Kosten und Zeitintervalle.
Die fraktale Struktur des Attraktors wird durch dynamische Fraktale verschiedener Ordnungen gebildet. Zu jedem Zeitpunkt befinden sich alle Fraktale, die eine fraktale Struktur bilden, in unterschiedlichen Stadien ihrer Fertigstellung – Fraktale einiger Ordnungen können vollständig abgeschlossen werden, andere Ordnungen – befinden sich in der Anfangsphase ihrer Bildung, dritte Ordnungen – in der Endphase und die vierte - in einer Zwischenstufe.
Abgeschlossen, d.h. Ein Fraktal ist ein Fraktal, bei dem alle drei Segmente nacheinander abgeschlossen sind. Die Vervollständigung des 3. Fraktalsegments ist die Vervollständigung des gesamten Fraktals.
Die Fertigstellung eines Fraktals bedeutet die Fertigstellung der Kosten- und Zeitintervalle seiner Segmente.
Das Kostenintervall eines Fraktales ist das Intervall zwischen dem Beginn der Projektion auf die Preisachse des 1. Fraktalsegments und dem Ende der Projektion seines 3. Segments.
Das Zeitintervall eines Fraktales ist das Intervall zwischen dem Beginn der Projektion auf der Zeitachse des 1. Fraktalsegments und dem Ende der Projektion seines 3. Segments. Das Zeitintervall eines Fraktales ist die Summe der Zeitintervalle aller drei seiner Segmente.
Die Stränge der fraktalen Struktur des Attraktors sind horizontale Ebenen, die durch die in jedem Monat gebildeten Extremumpunkte gezogen werden. Die Anzahl der Strings in einer fraktalen Struktur entspricht der doppelten Anzahl von Monaten, die für ihre Bildung benötigt wurden.
In den allermeisten Fällen werden Beginn und Ende der Kostenintervalle in der Nähe der auf den Saiten liegenden Punkte liegen.
Die Länge des Kostenintervalls ist ein absoluter Wert und die Länge des Zeitintervalls ist ein relativer Wert.
Zeit ist eine Form des Entstehungsprozesses einer fraktalen Struktur und eine Bedingung für die Möglichkeit ihrer Veränderung.
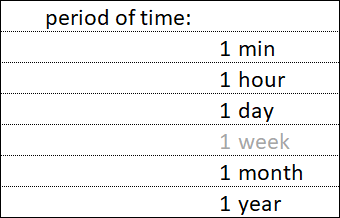
Alle diese einfachen Zeiträume, mit Ausnahme der Woche, sind Vielfache voneinander. Somit enthält eine Jahresperiode eine ganze Zahl von Monatsperioden, eine Monatsperiode enthält eine ganze Zahl von Tagesperioden, eine Tagesperiode enthält eine ganze Zahl von Stundenperioden und eine Stundenperiode enthält eine ganze Zahl von Minutenperioden.
Die Zeitintervalle der gebildeten Fraktale sind relativ zu einfachen Zeiträumen ungleichmäßig angeordnet, jedoch mit einem bestimmten Muster.
Der Anfang und das Ende eines Zeitintervalls können mit dem Anfang und dem Ende eines einfachen Zeitintervalls zusammenfallen, aber in den allermeisten Fällen liegen Anfang und Ende eines Zeitintervalls in der Nähe von Punkten, die einfache Zeiträume entlang der goldenen Verhältnis mit Fibonacci-Koeffizienten von 0,382 und 0,618.
Um die fraktale Struktur eines Diagramms in separate Fraktale mit drei Segmenten zu zerlegen, reicht es nicht aus, Diagramme zu analysieren, die nach einfachen Zeiträumen aufgebaut sind - 1 Minute, 1 Stunde, 1 Tag, 1 Monat, 1 Jahr. Um die fraktale Struktur zu finden, müssen Sie die Diagramme analysieren, die auf allen möglichen Zeitrahmen aufgebaut sind.
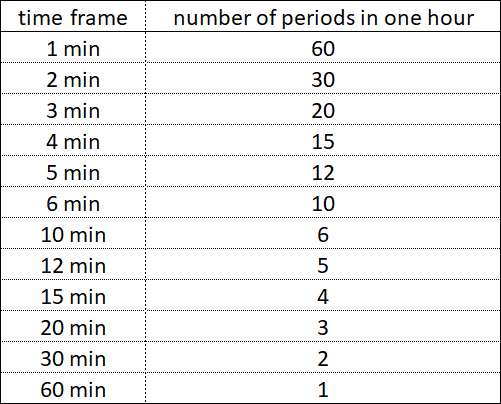
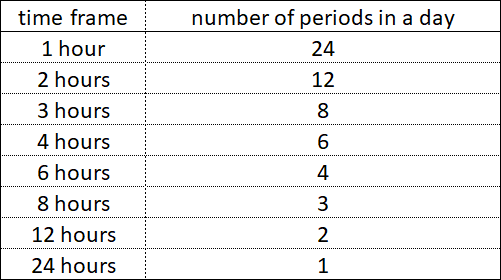
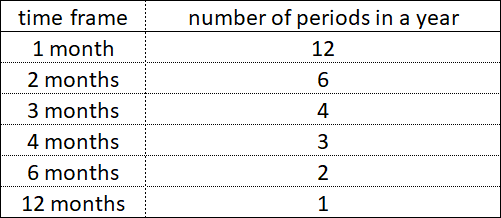
Innerhalb jedes einfachen Zeitraums - sei es 1 Stunde, 1 Tag oder 1 Jahr - gibt es kleinere Zeiträume, deren Bestandteile, die in bestimmten Zeitabständen gleichzeitig miteinander enden.
Innerhalb von 1 Stunde enden Zeiträume mit Zeitfenstern von 30 Minuten, 20 Minuten, 12 Minuten nicht gleichzeitig, aber Zeiträume mit Zeiträumen von 30 Minuten, 15 Minuten, 5 Minuten in einigen Zeitintervallen enden gleichzeitig.
Innerhalb von 1 Tag enden Zeiträume mit Zeitfenstern von 8 Stunden und 6 Stunden nicht gleichzeitig, aber Zeiträume mit Zeiträumen von 8 Stunden, 4 Stunden, 2 Stunden oder 12 Stunden, 6 Stunden und 3 Stunden in einigen Zeitintervallen enden gleichzeitig.
Innerhalb von 1 Jahr enden Zeiträume mit Zeiträumen von 4 Monaten und 3 Monaten nicht gleichzeitig, aber Zeiträume mit Zeiträumen von 6 Monaten und 2 Monaten enden in einigen Zeitintervallen gleichzeitig.
Die Zeiträume aller Zeitrahmen, die gleichzeitig beginnen, enden auch gleichzeitig mit dem Ende des einfachen Zeitbereichs.
Fraktale niedriger Ordnung bilden fraktale Strukturen auf Zeitintervallen mit täglichen Zeitrahmen, und fraktale Strukturen mit noch niedrigeren Fraktalen werden auf Zeitintervallen mit stündlichen Zeitrahmen gebildet.
Fraktale höherer Ordnung bilden fraktale Strukturen in Zeitintervallen mit monatlichen Zeitrahmen, und Fraktale höherer Ordnung bilden fraktale Strukturen in Zeitintervallen mit jährlichen Zeitrahmen.
Vervollständigungen von Kosten- und Zeitintervallen treten an Verzweigungspunkten auf, die in der überwiegenden Mehrheit der Fälle auf den Ketten fraktaler Strukturen liegen. Unter Berücksichtigung des Vorhandenseins einer großen Anzahl von Freiheitsgraden an Verzweigungspunkten in einem nichtlinearen dynamischen System führt die Modellierung der zukünftigen fraktalen Struktur über die zweiten Kosten- und Zeitintervalle hinaus zu einer großen Anzahl von Modellen, die oft die gleiche Implementierungswahrscheinlichkeit aufweisen, die es nicht erlaubt, ein einzelnes Modell als das wahrscheinlichste für die Implementierung zu wählen.
Eine genauere Vorhersage der zukünftigen Wertdynamik von Finanzinstrumenten wird durch die Analyse und Modellierung der fraktalen Struktur ihrer Charts zwischen zwei am nächsten beieinander liegenden Bifurkationspunkten, d.h. nur in den aktuellen Kosten- und Zeitintervallen - in Richtung der Bildung entweder des 1. Segments oder des 2. Segments oder des 3. Segments des Fraktales.
Für die kurzfristige Vorhersage der Wertdynamik von Finanzinstrumenten ist es notwendig, die fraktale Struktur von Charts zu simulieren, die auf Minuten- und Stundenrahmen aufgebaut sind.
Für die mittelfristige Prognose der Wertdynamik von Finanzinstrumenten ist es notwendig, die fraktale Struktur von Charts zu simulieren, die auf täglichen und wöchentlichen Zeitrahmen aufbauen.
Für die langfristige Vorhersage der Wertdynamik von Finanzinstrumenten ist es notwendig, die fraktale Struktur von Charts zu simulieren, die auf monatlichen und jährlichen Zeitrahmen aufbauen.
Der Prognosehorizont ist in allen drei Varianten gleich - die aktuellen Kosten und die aktuellen Zeitintervalle des entstehenden Fraktals, d.h. seine ersten, zweiten oder dritten Segmente bilden.
Auf Charts mit stündlichen Zeitrahmen ist der Prognosehorizont jedoch ein Zeitraum von mehreren Tagen oder Wochen, auf Charts mit täglichen und wöchentlichen Zeitrahmen ist der Prognosehorizont ein Zeitraum von mehreren Monaten, aber auf Charts mit monatlichem und jährlichem Zeitrahmen, wird der Prognosehorizont mehrere Jahre und sogar Jahrzehnte betragen.
Die Kostenintervalle von Fraktalen, unabhängig von ihrer Reihenfolge, neigen dazu, an Punkten zu enden, die entweder an Punkten liegen, die auf den Strings der Fraktalstruktur liegen, oder an Punkten, die gemäß den Fibonacci-Koeffizienten von den Strings entfernt liegen.
Zeitintervalle von Fraktalen, deren Ordnung niedriger als die höchste ist, neigen zur Vervollständigung in der Nähe der Endpunkte von Zeitintervallen, die gemäß den Fibonacci-Verhältnissen in einfachen Zeiträumen liegen.
Die Überlappung der Endpunkte der Kosten- und Zeitintervalle von Fraktalen bilden Bifurkationspunkte, die die Werte der zukünftigen Kosten- und Zeitintervalle neuer Fraktale vorgeben.
Die Vorhersage der Wertdynamik für einen langfristigen Zeitraum erfordert eine Analyse von fraktalen Strukturen, die durch Fraktale der höchsten und höchsten Ordnung gebildet werden, wobei sich die Bildung von Bifurkationspunkten von den fraktalen Strukturen unterscheidet, die durch Fraktale der Ordnung unter der höchsten Ordnung gebildet werden.
Die Vervollständigung der Zeitintervalle von Fraktalen höchster und höchster Ordnung erfolgt in der Nähe der Punkte, an denen die maximale Anzahl von Jahreszeiträumen gleichzeitig endet:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 und 34.
Besonderes Augenmerk sollte auf die gleichzeitige Beendigung von Jahreszeiträumen gelegt werden, darunter Fibonacci-Zeiträume: 1, 2, 3, 5, 8, 13, 21, 34.
Im Zeitintervall von 1 Jahr bis 40 Jahren beträgt die maximale Anzahl gleichzeitiger Beendigungen von Zeitrahmen 8.
Es gibt 8 gleichzeitige Endungen im 24, 30 und 36 Jahr.
Im 24 Jahr enden gleichzeitig folgende Jahreszeiträume:
1, 2, 3, 4, 6, 8, 12, 24.
Im 30 Jahr enden gleichzeitig folgende Jahreszeiträume:
1, 2, 3, 5, 6, 10, 15, 30.
Im 36 Jahr enden gleichzeitig folgende Jahreszeiträume:
1, 2, 3, 4, 6, 9, 12, 18.
Im Zeitraum 1 bis 2200 reicht die Anzahl der gleichzeitigen Fertigstellungen des Zeitrahmens in den Jahren 1 bis 34 von 1 bis 18.
18 ist die maximale Anzahl gleichzeitiger Abschlüsse in dieser Zeitspanne, die 1680 auftritt. In diesem Jahr werden folgende Zeitrahmen gleichzeitig absolviert: 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 16, 20, 21, 24, 28, 30.
Die Anzahl der gleichzeitigen Fertigstellungen von Zeitrahmen im Intervall (1; 2200) von 1 bis 9 beträgt 93,09 %, die restlichen 6,91 % entfallen auf die Anzahl der gleichzeitigen Fertigstellungen von 10 bis 18.
Das Ende der Zeitintervalle der Fraktale höchster Ordnung tritt in den Zeitintervallen ein, in denen die Anzahl gleichzeitiger Zeitrahmenvervollständigungen im Bereich von 10 bis 18 liegt.
Eine Zusammenfassung der gleichzeitigen Fertigstellung der Zeiträume in den Jahren 1 bis 34 für den Zeitraum 1 bis 2200 ist in der folgenden Grafik und Tabelle dargestellt.
Bei der Analyse von Zeitintervallen von Fraktalen höchster Ordnung wird das unvollendete Jahr auf das abgeschlossene aufgerundet, was eine genauere Analyse nicht erlaubt.
Um Zeitintervalle mit einer Genauigkeit von bis zu einem Monat zu analysieren, ist es notwendig, analog zu Jahreszeiträumen monatliche Zeiträume von 1 bis 34 für einen Zeitraum von 1 Jahr bis 2100 zu konstruieren und Zeitintervalle zu finden, in denen die maximale Anzahl von Zeiträumen mit unterschiedlichen Monatsenden zu gleichen Zeiträumen.
In diesem Fall wäre der Dezember 2000 ein 24000-Monat, der Dezember 2100 ein 25200-Monat und der Juli 2021 ein 24247-Monat.
Das Zeitintervall 1-2100 umfasst 25'200 Monate. In diesem Zeitintervall variiert die Anzahl der gleichzeitigen Fertigstellungen des Zeitrahmens in den Monaten 1 bis 34 von 1 bis 21 (21/34 = 0,618 - der „goldene Schnitt“).
21 ist die maximale Anzahl gleichzeitiger Abschlüsse in diesem Zeitintervall, die in den folgenden Jahren auftritt: 840, 1260, 1540, 1680 und 2100.
Die Anzahl der gleichzeitigen Fertigstellungen von Zeitrahmen im Intervall (1; 25200) von 1 bis 9 beträgt 92,96 %, die restlichen 7,04 % entfallen auf die Anzahl der gleichzeitigen Fertigstellungen von 10 bis 21.
Das Ende der Zeitintervalle der Fraktale höchster Ordnung tritt in den Zeitintervallen ein, in denen die Anzahl gleichzeitiger Zeitrahmenvervollständigungen im Bereich von 10 bis 21 liegt.
Eine Zusammenfassung der gleichzeitigen Fertigstellung der Zeitrahmen in den Monaten 1 bis 34 für den Zeitraum 1 bis 2100 ist in der folgenden Grafik und Tabelle dargestellt.
Bezeichnen wir das Zeitintervall als (1; L). wobei L∈N.
ТF - Zeitrahmen, ein Zeitraum, der sich im Intervall mehr als 1 Mal wiederholt (1; L). TF∈N.
m - gleichzeitiges Ende verschiedener Zeitrahmen im Intervall (1; L). m ∈ N.
nm - die Anzahl der gleichzeitigen Enden verschiedener Zeitrahmen im Intervall (1; L). n ∈ N.
Zuvor wurde die Verteilung von nm für TF = 34 in zwei Intervallen für L1 = 2’200 und L2 = 25’200 gezeigt.
Betrachten Sie die Verteilung von nm für das Intervall, in dem L3 = 252’000 ist.
Das Auf und Ab der Geschäftstätigkeit prägt das Auf und Ab der Wirtschaft und bezeichnet Konjunkturzyklen, die aus wiederholten Rezessionen, Depressionen und Belebungen der Wirtschaft bestehen.
Die Dynamik des Finanzmarktes erfolgt in Korrelation mit Konjunkturzyklen. Veränderungen in der Richtung der Dynamik der Werte von Aktienindizes, Währungsnotierungen und Rohstoffkosten zeigen das Ende einiger Wirtschaftszyklen und den Beginn anderer.
An den Zeitpunkten, an denen Zeiträume in den Jahren 1 bis 34 gleichzeitig in Höhe von mehr als 10 Fertigstellungen enden, kommt es zu Veränderungen der Konjunkturzyklen. In der Nähe dieser Punkte werden Bifurkationspunkte in der fraktalen Struktur der Graphen der Wertdynamik von Finanzanlagen gebildet, in denen einige Fraktale enden und andere beginnen.
Um die Dynamik wirtschaftlicher Prozesse zu simulieren, ist es erforderlich, die fraktalen Strukturen der Charts zu analysieren, die gemäß den folgenden jährlichen Fibonacci-Zeitrahmen aufgebaut sind:
1, 2, 3, 5, 8, 13, 21, 34, 55 und 10 Jahre.
Die Überlagerung von Zeitintervallen mit gleichzeitiger Vervollständigung einer großen Anzahl von Zeiträumen von 1 Jahr bis 34. über Zeitintervalle mit gleichzeitiger Vervollständigung einer großen Anzahl von Zeiträumen von 1 Monat bis 34. gibt ein klares Verständnis dafür, wo die Zeitintervalle der wird auf höchstem Niveau enden.
Gleichzeitiges Ende von Zeitrahmen innerhalb eines Zeitintervalls erfolgt an bestimmten Daten, die vom Beginn des Intervalls an gezählt werden.
Die moderne Chronologie stammt aus dem Jahr, in dem er auf der Erde in einem menschlichen Körper in einer seiner drei Hypostasen geboren wurde - der Sohn Gottes, unser Gott Jesus Christus.
Es gibt keine klaren und eindeutigen Tatsachen, die die Geburt unseres Gott Jesus Christus in dem Jahr bestätigen, auf dem die moderne Chronologie basiert. Für den Glauben und für das Heil der menschlichen Seele ist jedoch nicht das Geburtsjahr wichtig, sondern die Unbefleckte Empfängnis und Geburt Jesu Christi, sein Leben und seine Lehren, seine Kreuzigung und sein Leiden, seine Auferstehung aus dem tot und seine Himmelfahrt.
Es gibt viele Argumente, die auf die Geburt des Sohnes Gottes Jesus Christus 5 Jahre früher hinweisen, als allgemein angenommen wird.
Unter Berücksichtigung der Unsicherheit bezüglich des Beginns der modernen Chronologie muss bei der Analyse des gleichzeitigen Abschlusses der Jahresintervalle zur Identifizierung der Zeitintervalle, auf denen die globalen Bifurkationspunkte gebildet werden, dieser Tatsache Rechnung getragen werden.
Angesichts dieser Tatsache könnte das laufende Jahr 2021 das Jahr 2026 sein.
Lassen Sie uns die jährlichen Zeitrahmen von 1 bis 144 (12²) erstellen und die Zeitintervalle finden, in denen die maximale Anzahl ihrer gleichzeitigen Vervollständigungen vorhanden ist, wobei wir besonders auf die Zeitintervalle achten, in denen die Fibonacci-Zeitrahmen enden, und auf den Unterschied zwischen ihnen achten die Zeitintervalle gleich 5 Jahre.
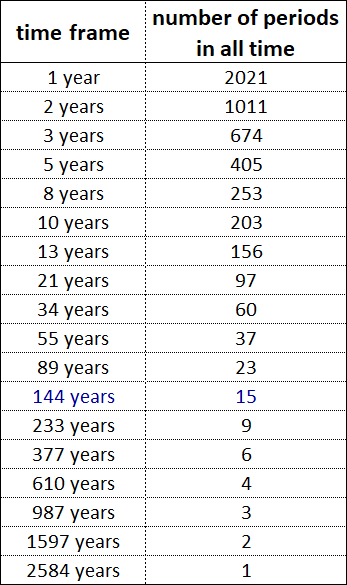
Die Scheitelpunkte der angegebenen Parabeln liegen in der Nähe des Zeitintervalls von 2021 bis 2026. Unter Berücksichtigung der allgemein anerkannten Zeitrechnung entspricht die Obergrenze der Bandbreite dem aktuellen Jahr 2021. Wenn die Zeit ab 5 v. Chr. ist, dann ist das aktuelle Jahr 2026, was dem unteren Ende der Spanne entspricht.
Angesichts der Unklarheit über den Beginn der modernen Chronologie ergibt sich eine Situation, in der die aktuelle Zeit entweder am Anfang des Zeitraums 2021-2026 oder an seinem Ende steht.
Das Zeitintervall 2021-2026, in das die Scheitelpunkte der angegebenen Parabeln fallen, ist ein Intervall, in dessen Nähe die maximal mögliche Anzahl von Zeitrahmen in Jahren vom 1. bis zum 144. endet, was den Abschluss höherer Ordnung anzeigt Fraktale in diesem Zeitintervall.
Auf den Zeitbereich 2021-2026, in dessen Nähe + - 2 Jahre, 56 Zeiträume enden, folgt das Jahr 2040, in dem 23 Zeiträume gleichzeitig enden, was das Ende der Zeitintervalle anzeigt von Fraktalen höchster Ordnung.
2021-2026 ist der Anfang der Endzeit. Fraktale höherer Ordnung, die in diesem Zeitraum begannen, werden die Fraktale höchster Ordnung bis 2040 vervollständigen.
2040 ist ein Meilensteinjahr, nach dem sich in fraktalen Strukturen neue Fraktale immer höherer Ordnung zu bilden beginnen.
3.20. Das Wesen der Modellierungsmethode.
Dabei können Sie mit Zeitintervallen den theoretischen Teil abschließen und vervollständigen, indem Sie das Wesen der Methode zur Modellierung der Wertdynamik von Finanzanlagen bestimmen, die darin besteht, die fraktale Struktur des Finanzanlagengraphen zu identifizieren und mit Attraktoren zu beschreiben aus dem Niro-Alphabet.
Der Prozess der Bildung der fraktalen Struktur des Attraktors durch dynamische Fraktale ist zyklisch, das heißt vorhersehbar, d.h. es ist möglich, die zukünftige Dynamik der Notierungen beliebiger Finanzinstrumente zu simulieren.
In den Diagrammen der Wertdynamik auf dem Finanzmarkt gibt es einen Zyklus, der in der Bildung eines Fraktales besteht und ausgedrückt wird in:
1. Bildung des 1. Segments des Fraktals.
2. Bildung des 2. Segments des Fraktales, das in die entgegengesetzte Richtung zum 1. gerichtet ist.
3. Bildung des 3. Segments des Fraktals, das die gleiche Richtung wie das 1. hat.
Nach Abschluss dieses Zyklus beginnt genau der gleiche Zyklus, jedoch in die entgegengesetzte Richtung. Alle diese Aktionen werden auf unbestimmte Zeit fortgesetzt - das erste Segment wird immer durch das zweite Segment ersetzt, das zweite Segment wird immer durch das dritte Segment ersetzt und das dritte Segment wird immer durch das erste Segment ersetzt.
Die zyklische Natur des Prozesses der Bildung von Fraktalen und der fraktalen Struktur in Übereinstimmung mit einer bestimmten Reihenfolge gibt ein Verständnis dafür, welches Segment des Fraktals und in welche Richtung gebildet wird, nachdem die Bildung des aktuellen Segments abgeschlossen ist.
Zu jedem Zeitpunkt bildet sich die Wertdynamik eines finanziellen Vermögenswerts in einem der drei fraktalen Segmente - dem ersten, zweiten oder dritten. Nach dem ersten Segment des Fraktals wird immer das zweite Segment des gleichen Fraktals gebildet, danach wird immer das dritte Segment des gleichen Fraktals gebildet, und dann beginnt sich wieder das erste Segment zu bilden, jedoch bereits von einem anderen Fraktal, das entweder die gleiche oder eine größere, und die notwendigerweise in die entgegengesetzte Richtung des vorherigen Fraktals gerichtet ist.
Die Extrempunkte auf dem Diagramm sind die Punkte, an denen entweder das erste Segment endet und das zweite beginnt oder das zweite Segment endet und das dritte beginnt oder das dritte Segment endet und das erste beginnt. Die Extremumpunkte definieren die Grenzen der Kosten- und Zeitintervalle von Fraktalen in den fraktalen Strukturen von Attraktoren.
Die Proportionen zwischen den Werten der Kosten und Zeitintervalle der Segmente ermöglichen es Ihnen, Folgendes zu bestimmen:
- Welche Segmente sind das - das erste, zweite oder dritte,
- welche Arten und Arten von Fraktalen diese Segmente bilden und
- Wie ist die Reihenfolge der gebildeten Fraktale in der fraktalen Struktur zueinander.
Die Methode zur Modellierung der Dynamik von Notierungen von Finanzinstrumenten basiert auf der Bestimmung des aktuellen Fraktalsegments – des ersten, zweiten oder dritten, um zu bestimmen, welches Segment des Fraktals das nächste nach dem aktuellen sein wird.
Das Alphabet der Niro-Attraktoren besteht aus 15 Fraktalen:
11, 12, 13, 14, 15; 21, 22, 23, 24, 25; 31, 32, 33, 34, 35;
die in drei Typen unterteilt sind, von denen jeder fünf Typen hat.
Jedes der 15 Fraktale ist ein Attraktor, den der Graph jedes nichtlinearen dynamischen Systems anstrebt.
Die Modellierung der zukünftigen Wertdynamik beginnt mit der Analyse der Hauptfraktalstruktur, die aus Fraktalen höchster Ordnung besteht, d. h. mit der Analyse von Diagrammen, die auf jährlichen Zeitrahmen aufgebaut sind. Im Rahmen der Analyse der Hauptfraktalstruktur wird ermittelt, zu welcher der 15 Attraktorentypen die Grafik der Dynamik des Finanzanlagewerts gehört.
Nachdem der Attraktor der Hauptfraktalstruktur identifiziert wurde, ist es möglich, nicht nur langfristige Vorhersagen der Wertdynamik, sondern auch mittelfristige und kurzfristige Vorhersagen zu treffen, da die Bildung von fraktalen Strukturen aus Fraktalen mit einer Ordnung unterhalb des höchsten wird in strikter Übereinstimmung und Unterordnung unter die Hauptfraktalstruktur auftreten.
Um die zukünftige Dynamik des Finanzmarktes klar zu erkennen, ist es daher notwendig, das Alphabet der Niro-Attraktoren zu kennen und es verwenden zu können, um die fraktalen Strukturen von Charts von Finanzinstrumenten zu lesen und zu beschreiben, die in den Währungen, Aktien und Rohstoffmärkte.
Das Niro-Alphabet schließt Apophenie von der Dynamik des Finanzmarktes aus und macht das Muster in der Dynamik des Wertes von Finanzanlagen klar und deutlich. In diesem Fall kann jeder ein Hellseher werden.
An dieser Stelle kann die Betrachtung der Hauptaspekte der Methode zur Modellierung der Wertdynamik auf dem Finanzmarkt abgeschlossen werden, vom theoretischen Teil zum praktischen übergehen und die Anwendung der Methode zur Modellierung der zukünftigen Dynamik auf eine spezifische Beispiel.
4. Modell der zukünftigen Dynamik der Dow Jones Indexwerte.
Als Beispiel für die Modellierung zukünftiger Dynamiken nehmen wir die Dynamik der Werte des amerikanischen Aktienindex Dow Jones.
Eine detaillierte und detaillierte Modellierung der Dynamik des Dow-Jones-Index wird im Artikel "Wann Wird Dow Low?" diskutiert, und hier ist ein bereits gebautes Modell der zukünftigen Dynamik, das derzeit die höchste Wahrscheinlichkeit der Umsetzung hat.
Entsprechend der fraktalen Struktur des Dow-Jones-Index zum Ende des ersten Halbjahres 2021 können wir sagen, dass die zukünftige Dynamik der Indexwerte in folgender Reihenfolge stattfinden wird:
1. Von 2021 bis 2028 wird die Dynamik des Dow Jones Index rückläufig sein, wodurch der Rückgang der Indexwerte bei 15'300 Punkten stoppen kann. Ein solcher Rückgang der Indexwerte wird durch die Vervollständigung des Fraktals 6. Ordnung F133313, das das 3. Segment des Fraktals 5. Ordnung F13331 ist, verursacht und tritt innerhalb der Bildung des Fraktals 5. Ordnung F13332 auf, das das 2. Segment ist des Fraktals 4. Ordnung F1333.
2. Von 2028 bis 2035 wird die Dynamik des Index nach oben gerichtet sein, um die im Jahr 2021 erreichten Höchstwerte zu wiederholen. Eine solche Erhöhung der Indexwerte erfolgt im Rahmen der Bildung des Fraktals 5. Ordnung F13333, das das 3. Segment des Fraktals 4. Ordnung F1333 ist.
3. Im Jahr 2035 wird ein globaler Rückgang des Dow-Jones-Index als Ergebnis der gleichzeitigen Vervollständigung der dritten Segmente von Fraktalen unterschiedlicher Ordnung beginnen: F13333, F1333, F133, F13, die das Fraktal der höchsten Ordnung F1 vervollständigen werden. Der Zusammenbruch des amerikanischen Aktienmarktes findet vor dem Hintergrund der Bildung des 2. Segments des F2-Fraktals höchster Ordnung statt. Dieser Rückgang könnte den Wert des Dow Jones Index auf 2'700 Punkte senken.
Unter Berücksichtigung der aufkommenden lokalen fraktalen Struktur ist davon auszugehen, dass innerhalb des Zeitintervalls (1978, 2035) die vier oben genannten Fraktale im Jahr 2035 gleichzeitig ihre Bildung abschließen: F1333, F133, F13, F1.
1. Fraktal F1333 ist ein Fraktal 4. Ordnung, es besteht aus Segmenten: F13331, F13332, F13333, die Fraktale 5. Ordnung sind und Fraktal Nr. 23 aus dem Niro-Alphabet sein können:
F1333 ≡ F23.
Prognostiziertes Zeitintervall T1333 - (2014, 2035).
Prognostiziertes Kostenintervall P1333 = 19750,86.
2. Fraktal F133 ist ein Fraktal 3. Ordnung, es besteht aus Segmenten: F1331, F1332, F1333, die Fraktale 4. Ordnung sind und Fraktal Nr. 11 aus dem Niro-Alphabet sein können:
F133 ≡ F11 → FS {13, MS, 23}.
Prognostiziertes Zeitintervall T133 - (2001, 2035).
Prognostiziertes Kostenintervall P133 = 27164,66.
3. Fraktal F13 ist ein Fraktal 2. Ordnung, besteht aus Segmenten: F131, F132, F133, die Fraktale 3. Ordnung sind und Fraktal Nr. 11 aus dem Niro-Alphabet sein können:
F13 ≡ F11 → FS {11, MS, 11}.
Voraussichtliches Zeitintervall T13 - (1978, 2035).
Prognostiziertes Kostenintervall P13 = 34354,76.
4. Fraktal F1 ist ein Fraktal der höchsten 1. Ordnung, besteht aus Segmenten: F11, F12, F13, die Fraktale 2. Ordnung sind und Fraktal Nr. 11 aus dem Niro-Alphabet sein können:
F1 ≡ F11 → FS {13, 23, 11}.
Prognostiziertes Zeitintervall T1 - (1896, 2035).
Prognostiziertes Kostenintervall P1 = 35.062,90.
Das Fraktal F13331 5. Ordnung begann sich im Oktober 2014 zu bilden und endete im Mai 2021. F13331 ist das erste Segment des Fraktals 4. Ordnung F1333, nach dessen Abschluss sich das Fraktal F13332 zu bilden beginnt, das das 2. Segment des Fraktals F1333 ist, und dann das F13333-Fraktal, das das dritte Segment des Fraktals F1333 ist.
Das zweite Segment F13332 des Fraktals F1333, das sich im Mai 2021 zu bilden begann, könnte seine Bildung im Jahr 2028 abschließen. Im Rahmen der Bildung des Fraktales F13332 können die Dow-Jones-Indexwerte bis 2028 auf das Niveau von 16.000 Punkten fallen.
Das 3. Segment F13333 des Fraktals F1333 kann sich im Zeitintervall von 2028 bis 2035 bilden. Im Rahmen der Bildung des Fraktals F13333 dürfen die Dow Jones Indexwerte wieder von der 16.000-Punkte-Marke auf die 36.000-Punkte-Marke steigen.
Die Fraktale F13333, F1333, F133, F13 sind die dritten Fraktalsegmente, in denen die Reihenfolge jedes nachfolgenden Fraktales eine Ordnung höher ist als das vorherige.
Mit der Vervollständigung des Fraktals 5. Ordnung F13333 wird die gleichzeitige Vervollständigung des Fraktals 4. Ordnung F1333 und des Fraktals 3. Ordnung F133 und des Fraktals 2. Ordnung F13 und des Fraktals F1 erster Ordnung erfolgen.
Das Fraktal 2. Ordnung F11 ist das 1. Segment des höchsten Fraktales 1. Ordnung F1. F11 wurde im Zeitraum von 1896 bis 1973 gebildet.
Das Fraktal 2. Ordnung F12 ist das 2. Segment des höchsten Fraktales 1. Ordnung F1. F12 wurde über den Zeitraum von 1973 bis 1978 gebildet.
Das Fraktal 2. Ordnung F13 ist das 3. Segment des höchsten Fraktales 1. Ordnung F1. F13 wird sich im Zeitintervall 1976 bis 2035 bilden.
Der Attraktor der fraktalen Struktur FS {13, 23, 11} des Dow-Jones-Indexgraphen ist also das F11-Fraktal - Fraktal Nr. 11 aus dem Niro-Alphabet, das vom 1. Typ ist und zum 1. Typ gehört.
Die Fertigstellung des F13-Fraktals im Jahr 2035 wird das F1-Fraktal vervollständigen. Damit endet der 1896 begonnene Wachstumszyklus des Dow-Jones-Index.
Im Jahr 2035 wird am amerikanischen Aktienmarkt ein globaler Abwärtstrend beginnen. Der Kursrückgang amerikanischer Aktien kann so stark ausfallen, dass der Wert des Dow-Jones-Index bis auf 2700 Punkte sinken wird. Dieser Rückgang findet innerhalb der Bildung des Fraktales F2 höchster Ordnung statt, das das zweite Segment in der globalen Fraktalstruktur ist.
5. Fazit.
Abschließend möchte ich anmerken, dass eine Person gewissermaßen ein komplexes biologisches nichtlineares dynamisches System ist, das andere nichtlineare dynamische Systeme hervorbringt, einschließlich des Finanzmarktes.
Das zukünftige Verhalten nichtlinearer dynamischer Systeme ist immer multivariat, dh es gibt immer mehrere alternative Attraktoren dieser Systeme. Es gibt nie ein einziges Szenario für die Entwicklung bestimmter Ereignisse, weder im Leben eines Menschen noch auf dem Finanzmarkt.
Die Ereignisse, die jetzt im Leben einer Person auftreten, und die Handlungen, die eine Person jetzt begeht, bestimmen jeweils die Ereignisse, die in der Zukunft auftreten werden, und die Handlungen, die in dieser Zukunft von ihr ausgeführt werden.
Die jetzt auftretenden Kursschwankungen am Finanzmarkt und die sich auf den Charts der Finanzanlagen bildenden Fraktale bestimmen nun direkt deren zukünftige Dynamik.
Das menschliche Gehirn ist ein biologischer Computer, der in strikter Übereinstimmung mit den in ihn geladenen Programmen und Algorithmen funktioniert, die sein Weltbild bilden, das sein Leben, seine Ansichten, Handlungen, Handlungen bestimmt.
Die oben diskutierte Methode zur Modellierung des Wertes auf dem Finanzmarkt kann als eine Art Computerprogramm oder eine Art Algorithmus angesehen werden, der Ihr Gehirn "lädt", mit dem Sie sehen und verstehen können, dass nichts Zufälliges und chaotisch auf dem Finanzmarkt passiert und dass die Dynamik der Notierungen finanzieller Vermögenswerte vom Betreiber N geordnet und definiert wird.
 — Бесплатные Сайты и CRM.
— Бесплатные Сайты и CRM.