Апофения как апологет ясновидения на рынках капитала.
Оглавление.
1. Вступление.
2. Парадигма: линейная vs нелинейная.
3. Метод моделирования динамики стоимости на финансовом рынке.
3.1. Предисловие.
3.2. Финансовый рынок – это НДАСС.
3.3. Стоимость есть функция времени: P=N(T).
3.4. Фрактал и фрактальная структура.
3.5. Порядок, виды и типы фракталов.
3.6. Базисный фрактал.
3.7. Общий вид фрактальной структуры.
3.8. Динамика базисного фрактала.
3.9. Описание фрактальной структуры.
3.10. Определение порядка и хаоса.
3.11. Порядок фракталов.
3.12. Нумерация фракталов.
3.13. Определение точек экстремумов.
3.14. Виды и типы фракталов.
3.15. 15 фракталов:
3.15.1. Фракталы 1-го вида;
3.15.2. Фракталы 2-го вида;
3.15.3. Фракталы 3-го вида.
3.16. Пропорции между сегментами фракталов.
3.17. Азбука аттракторов Niro.
3.18. Точка бифуркации и степени свободы.
3.19. Стоимостные и временные интервалы.
3.20. Суть метода моделирования.
4. Модель будущей динамики значений индекса Dow Jones.
5. Заключение.
В данной статье описан метод моделирования будущей динамики стоимости финансовых активов.
Метод основан на теории хаоса и фрактальной геометрии.
Апофения – это способность видеть структуру, взаимосвязь, закономерность там, где они не очевидны или скрыты.
Во Вселенной всё закономерно. Закономерность присутствует везде и во всём непрерывно.
Закономерность всегда скрытна, поэтому фраза “Здесь нет закономерности!” говорит не об её отсутствии, а о том, что закономерность пока ещё не обнаружена. Обнаруживается закономерность только в процессе её поиска.
В статье рассказывается о возможности прогнозирования динамики финансового рынка и методе моделирования динамики котировок финансовых активов.
Ясновидение финансового рынка – это не про сверх способности из разряда чего-то сверх естественного. Ясно видеть будущую динамику котировок валют, акций, облигаций, фьючерсов и опционов под силу каждому.
Задача моделирования динамики котировок не сложнее задачи решения квадратного уравнения. Метод моделирования так же, как и метод нахождение корней квадратного уравнения предполагает совершение понятного алгоритма действий.
Ясное видение динамики финансового рынка вытекает из ясного видения в хаотических колебаниях стоимости финансовых активов закономерной динамики, структурируемой в соответствии с определённым порядком.

Экономическая теория, которая сложилась в прошлом веке, с господствующей линейной парадигмой не способна объяснять происходящие в экономике процессы и не позволяет предвидеть их будущее развитие, оставляя без ответов вопросы механизма ценообразования на рынках капитала.
Динамика стоимости на финансовом рынке, подверженная внезапным и резким колебаниям, не объясняется ни гипотезой эффективного рынка, ни какими-либо другими гипотезами, которые выдвигаются экономистами традиционной классической школы.
Исследования рынков капитала в разрезе их функционирования заставляют искать новые подходы к поиску механизма ценообразования, в котором научные знания будут совпадать с объективной реальностью.
Всё более очевидной становится необходимость введения новой парадигмы, в которой бы теория объясняла будущую динамику стоимости на финансовом рынке, а объективная реальность это подтверждала бы. Как раз о такой теории, описывающей механизм, приводящей стоимость на финансовом рынке в динамику, пойдёт речь в этой статье.
Нелинейные динамические системы, теория хаоса, фрактальная геометрия, синергетика – это те направления научных мыслей, которые в отношении динамики стоимости на финансовом рынке дают объяснение и понимание тому, что происходило, что происходит и что будет происходить с динамикой котировок финансовых инструментов.
Динамика стоимости финансовых инструментов, складывающаяся на электронных торгах и торгах фондовых бирж, не является хаотической, потому что подчинена определённому закону, который позволяет её прогнозировать. Соответственно прогнозируемой является и динамика всего финансового рынка.
Основанный на этом законе метод прогнозирования позволяет моделировать будущую динамику стоимости финансовых активов и на основе составленных моделей принимать эффективные инвестиционные решения реально управляя рыночным риском.
В более широком смысле можно сказать, что метод прогнозирования – это вычислительная технология для моделирования поведения нелинейных процессов в социальных динамических системах, которыми являются финансовые рынки как часть экономики.
Моделирование динамики финансового рынка предполагает на основе анализа временных рядов определять модели будущей динамики котировок финансовых инструментов (валют, акций, индексов, деривативов и пр.), а затем проводить их фильтрацию с целью отбора наиболее вероятных сценариев развития.
Модель будущей динамики стоимости финансового актива представляет собой описание наиболее вероятных траекторий движения цены на графике, которые актуальны на момент составления.
2. Парадигма: линейная vs нелинейная.
Парадигма – это умозрительная модель, позволяющая рассматривать явления в глобальном аспекте.
Сначала вкратце рассмотрим общепринятую теорию рынков капитала в линейной парадигме с обозначением её преимуществ и недостатков, а затем обозначим превосходство нелинейной парадигмы для описания динамики финансового рынка.
Преимущество линейной модели состоит в её простоте, поэтому с линейными моделями легче работать, закрыв глаза на кроющиеся в её ограничениях опасности появления ошибок в расчётах.
Чтобы сделать финансовые рынки более понятными экономисты создали объясняющие модели, которые не отражают реальность в полном объёме. С помощью нескольких упрощающих предположений о поведении инвесторов была создана общая аналитическая модель в линейной парадигме, которая не отличается хорошей работой, но зато объясняет некоторые явления и процессы в экономике, оставляя при этом многое неясным и необъяснимым.
Так, например, обнаруживается, что экономические прогнозы имеют ограниченную эмпирическую валидность, то есть построенные экономические модели будущего отражают действительность только в коротком временном интервале, потому что незначительное изменение только одной переменной имеет огромное влияние на будущий результат.
Более того, всё чаще обнаруживается, что стоимость на финансовом рынке на самом деле ведёт себя не так, как того требует теория случайных блужданий, которую применяют экономисты в своих расчётах.
На рынках происходит намного больше сильных скачков цен, чтобы их можно было объяснять исключением из правил в виде эффектов шума.
На этапе зарождения и развития эконометрики как науки предполагалось появление возможностей точного прогнозирования развития экономических процессов с целью предупреждения и избегания экономических кризисов или их негативных последствий.
Сегодня же экономические прогнозы часто являют собой объект издевательств и насмешек, потому что ни о каком их предсказательном эффекте говорить не приходится.
Откуда же проистекают ошибки, где они кроются, и почему современная экономическая теория не позволяет предвидеть кризисы в экономике, чтобы соответствующим образом к ним готовиться? В чём же проблемы?
Во-первых, одной из проблем является существующая в экономической теории концепция равновесия. Эконометрический подход предполагает, что если не существует внешних воздействий, то система находится в покое, то есть в состоянии равновесия, при котором всё уравновешивает друг друга. Например, предложение равно спросу.
Появляющиеся экзогенные факторы, возмущая систему, выводят её из равновесия. Система реагирует на возмущение и возвращается в равновесное положение линейно и немедленно, потому что она всегда стремится быть в равновесии и не приемлет разбалансированности. Для поддержания концепции равновесия введено понятие эффективного рынка, согласно которому все активы оцениваются справедливо, т.е. с использованием всей информации, которая доступна всем без исключения участникам рынка, которые к тому же несклонны к рискам в инвестиционной деятельности.
Однако, все эти допущения о равновесии, о всеобщей доступности информации, об игнорировании рисков, мягко говоря, “притянуты за уши” и не соответствуют реальному положению дел.
Рыночная экономика является эволюционирующей системой, попытки контролировать которую, управлять и держать в равновесии, обречены на провал. С регулярной частотой сваливающиеся на нас как снег на голову экономические кризисы – тому хорошее подтверждение.
Во-вторых, немаловажной проблемой для эконометрического взгляда на мир является время. Эконометрика игнорирует время, т.е. экономика и рынки при таком подходе не обладают памятью о прошлом или имеют очень ограниченную память. В лучшем случае эконометрика признаёт короткую память. Считается, что эффекты памяти быстро диссипируют.
Идея о том, что одно какое-то событие может бесконечно долго влиять на будущее, чужда эконометрике. Реальное же положение дел указывает на обратное. Влияние на развитие экономики и динамики финансового рынка в настоящем и будущем оказывают абсолютно все события, которые когда-либо произошли в прошлом независимо от срока давности – хоть день назад, хоть неделю назад, хоть месяц назад, хоть годы, десятилетия и века назад.
Теория рынков капитала в линейной парадигме основывается на следующих концепциях:
1. Рациональные инвесторы.
Рациональные инвесторы стремятся к получению среднестатистической прибыли с уровнем риска, который измеряется как стандартное отклонение. Предпочтение отдаётся активам, которые дают наивысшую ожидаемую доходность при заданном уровне риска. Инвесторы не склонны к риску и всячески его избегают.
2. Эффективный рынок.
Эффективный рынок подразумевает, что информация немедленно отражается в ценах, которые формируются всеми участниками рынка, имеющими к ней равный доступ.
3. Случайные блуждания.
В соответствии с двумя выше указанными концепциями цены и, как следствие прибыли, следуют случайному блужданию, т.е. их вероятностное распределение нормально, что означает возможность применения закона нормального распределения случайной величины и расчёта математического ожидания с дисперсией.
Линейная парадигма предполагает, что инвесторы линейно реагируют на информацию, используя её сразу после получения и не ожидая её накопления в ряде последующих событий. Линейный взгляд соответствует концепции рационального инвестора, которая утверждает, что прошлая информация уже дисконтирована и отражена в ценах. Таким образом, линейная парадигма подразумевает, что прибыли должны иметь приблизительно нормальное распределение и быть независимыми.
Нелинейная парадигма рассматривает все возможные реакции инвесторов на информацию, как линейные, так и не линейные, что увеличивает количество возможных сценариев развития ситуации.
Результаты исследований временных рядов различных финансовых активов показывают, что цены не следуют нормальному распределению, поэтому нельзя к ним применять теорию случайных блужданий и использовать методы статистического анализа в расчётах.
Чрезмерная волатильность стоимости на рынках бросает вызов:
• идее рациональных инвесторов;
• концепции, утверждающей, что благодаря большому количеству участников рынка можно достичь рыночной эффективности.
Случайное блуждание необходимо для применения статистического анализа к временным рядам ценовых изменений, чтобы теория портфеля имела право на существование. Без нормального распределения в линейной парадигме теоретические и эмпирические выкладки лишены всякого смысла.
Теория эффективного рынка базируется на постулате рациональности инвесторов. Рациональность определяется формированием цены на основе всей доступной информации. Под рациональностью подразумевается также, что инвесторы не расположены к риску. Но разве рациональны люди во всей своей совокупности в целом, если отталкиваться от этого определения рациональности? Конечно же нет!
Рассмотрим, как реагируют люди, когда стоят перед выбором получения убытка или прибыли.
Общепринятая теория гласит, что инвесторы не любят рисковать. И если кто-то идёт на большой риск, то этот риск должен быть компенсирован возможностью получения большой прибыли.
Всевозможные исследования показывают, что когда потери приемлемы, то люди идут на риск и становятся больше похожи на азартных игроков, нежели на рациональных инвесторов.
Приведём пример, показывающий изменение аппетита к риску.
Предположим, инвестор имеет выбор между:
1) Гарантированным заработком 85’000 $ или
2) 85%-ой возможностью заработать 100’000$ и 15%-ой возможностью не заработать ничего.
Большинство инвесторов предпочтут гарантированный доход в 85’000$, хотя ожидаемая прибыль в обоих случаях одинакова и составляет 85’000$. Такой выбор подтверждает несклонность инвесторов к рискам.
Если же предложить сделать выбор между:
1) Гарантированной потерей 85’000$ или
2) 85% шансов потерять 100’000$ и 15% - не потерять ничего?
то тогда, несмотря на одинаковый ожидаемый убыток в обоих случаях, люди уже будут рисковать и шанс избежать потерь будет предпочтительнее, чем шанс понести гарантированный убыток, даже если вероятность этого будущего убытка будет велика. Формулировка поменялась и теперь инвесторы стремятся рисковать.
Теория эффективного рынка предполагает также, что все инвесторы имеют одинаковый горизонт инвестирования. Это допущение необходимо для того, чтобы ожидаемые прибыли были сравнимы. Но хорошо известно, что в реальности это не так.
Когда предлагается возможность получения 10’000$ сейчас или 10’500$ через месяц, то большинство инвесторов предпочтут получить 10’000$ сейчас. Однако, если инвесторам предложить 10’000$ через год или 10’500$ через 13 месяцев, то большинство инвесторов выберут более длинный период времени, чтобы получить 10’500$. А это снова не совпадает с моделью рационального инвестора.
Особо следует обратить внимание на то, как люди ведут себя в условиях неопределённости. Гипотеза рациональности инвесторов утверждает, что их субъективные оценки рисков одинаковы. Однако, инвесторы в подавляющем своём большинстве склонны к чересчур самоуверенным своим оценкам и прогнозам. Мозг человека устроен таким образом, что принимает решения с высокой определённостью после получения информации в мизерном объёме.
Уверенность в принятии решений перед лицом неопределённости – стандартная ситуация для инвесторов. Однако, чрезмерная самоуверенность может стать причиной игнорирования важной информации, которая может быть использована другими. Следовательно, исходя из своих субъективных оценок, инвесторы склонны присваивать отдельным экономическим сценариям большую вероятность, чем это оправдано реальными фактами.
Так, например, если в некотором экономическом сценарии присваивается 60% росту, 30% - к отсутствию роста, а 10% - спаду, то в реальности инвестор, который уверен в сценарии роста, предпочтёт увеличить эту вероятность до 90%, а 10% оставить на вялый рост, чтобы не выглядеть слишком уверенным. Про спад же будет сказано, что он не представляется на данный момент возможным.
Наблюдения за инвесторами показывают, что они не реагируют и не следуют начавшимся трендам на рынках до тех пор, пока эти тренды явно не проявятся и не установятся. Инвесторы не экстраполируют происходящие на рынках явления и события в течение некоторого времени их развития, после чего принимают решения, которые обусловлены накопленной информацией, игнорируемой до некоторого момента времени. Такое поведение инвесторов коренным образом отличается от предполагаемых действий рациональных инвесторов, которые должны немедленно руководствоваться всей новой информацией.
Инвесторы склонны быть слишком самоуверенными в своих собственных прогнозах, поэтому игнорируют важную информацию, если она не совпадает с их мнением. Инвесторы не отказываются от своих прогнозов до тех пор, пока не получат достаточно информации об изменении ситуации.
Если инвесторы реагируют именно таким образом, то рынок не может быть эффективным, потому что вся информация не отражается в рыночных ценах. Многое, в таком случае, остаётся в ценах не учтённым, и реакция инвесторов на произошедшие события наступает позже и ни о какой линейности говорить не приходится.
Когда отдельные инвесторы не склонны быть столь рациональными, то нет никаких оснований полагать, чтобы дело обстоит иным образом во всём инвесторском сообществе.
Если инвесторы игнорируют информацию до тех пор, пока тренды не установятся, а затем, принимая в расчёт всю накопившуюся информацию, используют её в принятии решений, то это означает, что реакция на информацию происходит нелинейно. Как только объём накопившейся информации превысит некий критический уровень, то сразу же начинает сказываться всё её совокупное влияние, которое до того не влекло за собой никаких последствий. Это говорит о прямом влиянии прошлого на настоящее и, следовательно, о полной несостоятельности теории эффективного рынка, в которой информация и отклик на неё находятся в жёсткой причинно-следственной связи, согласно которой полученная информация сразу же отражается в ценах.
Концепция рационального инвестора и гипотеза эффективного рынка, основанные на допущении независимости наблюдений и нормальном распределении были созданы для применения вероятностных расчётов в экономической теории. Применение этой концепции на практике показывает всю ошибочность этого упрощающего предположения о рациональном инвесторе, потому что объективная реальность не подтверждает сделанные расчёты и прогнозы.
Теория рынков капитала с линейной парадигмой игнорирует помимо не реалистичности рационального инвестора, отсутствия общедоступности информации и ненормального распределения ещё и предположение о том, что различные рынки и различные ценные бумаги связаны друг с другом.
В отличие от линейных систем нелинейные динамические системы – это системы в динамике которых:
- присутствует обратная связь, что означает зависимость происходящего в настоящем от происходившего в прошлом;
- существуют критические уровни, где имеет место больше чем одно положение равновесия;
- формируются динамические фракталы;
- имеет место чувствительная зависимость от начальных условий.
Всё перечисленное указывает на то, что финансовые рынки всё же являются нелинейными динамическими системами и тогда от них можно ожидать следующего:
1. Долговременных корреляций и трендов, т.е. эффектов обратной связи;
2. Изменчивости с критическими уровнями при определённых условиях и в определённое время;
3. Наличия фрактальной структуры временных рядов;
4. Уменьшения надёжности прогнозирования по мере увеличения временных интервалов, т.е. проявления чувствительной зависимости от начальных условий.
Выше перечисленное присуще системам, которые не являются равновесными и характерно для рынков, которые мы знаем из опыта и практики.
Теория эффективного рынка в линейной парадигме подобна облакам в форме куба, которые могут существовать только в головах оторванных от реальности теоретиков, экономические прогнозы которых никогда точными не будут потому что:
• Инвесторы не всегда питают отвращение к риску. Очень часто, почти всегда, инвесторы будут стремиться рисковать, если сознают, что без риска они обречены на потери.
• Субъективные оценки инвесторов полны предубеждений. Они уверены в своих собственных предсказаниях гораздо более того, чем это оправдано имеющейся информацией.
• Инвесторы могут не реагировать на информацию сразу по её получении. Вместо этого они могут откликаться на неё некоторое время спустя, если она подтверждает изменение в недавнем тренде, что говорит о нелинейности реакции.
• Не существует никаких доказательств и никакого подтверждения того, что инвесторы рациональны в совокупности, чем по отдельности.
Доминирование линейной парадигмы в отношении финансового рынка прекращается, потому что рынки показали со всей очевидностью, что редко бывают столь упорядоченными в нашем линейном представлении о них, так как весьма часто, особенно когда меньше всего ожидается, возникает экспоненциальная супер-реакция на воздействие, свидетельствующая о нелинейности реакции чем линейности.
Теория хаоса и науки о нелинейных динамических системах предлагают иной подход к описанию происходящего на финансовом рынке. Чтобы понимать прошлое, осознавать настоящее и видеть будущее в экономике, необходимо сменить линейную парадигму на нелинейную. На смену старым методам должны прийти новые, которые не предполагают независимости, рациональности, случайных блужданий и нормальности распределений.
Рынки должны рассматриваться как нелинейные динамические аддитивно-синергетические системы (НДАСС), а динамика стоимости должна описываться динамическими фракталами. Нелинейная парадигма должна допустить в теорию рынков концепцию долговременной памяти, постулирующей, что произошедшие события на рынки могут влиять бесконечно долгое время.
Изменения котировок финансовых инструментов, если они не вписываются в экономическую теорию с линейной парадигмой, как правило, объясняют подбором соответствующих логике новостей, а если таких новостей найти не удаётся, то всё остаётся без каких-либо объяснений с надеждой на появление будущих новостей, которые впишутся в логику произошедшего.
В отличие от линейной парадигмы, нелинейная парадигма всегда даёт ответ на вопрос о причинах той или иной динамики стоимости на финансовом рынке вне зависимости от финансового инструмента и рынка, на котором он торгуется.
Пора заканчивать с линейной парадигмой и переходить на рельсы нелинейной парадигмы, предлагающей возможность моделирования динамики стоимости на финансовом рынке.
3. Метод моделирования динамики стоимости на финансовом рынке.
3.1. Предисловие.
Прежде чем перейти непосредственно к рассмотрению метода моделирования динамики стоимости на финансовом рынке, сделаем небольшое вступление.
Теория нелинейных динамических систем создавалась для описания движения потоков частиц в физических средах – таких как газ, жидкость, плазма. При изменении величин внешних воздействий на систему, например, температуры или давления, теория позволяет описывать и моделировать в соответствии с параметрами внешних воздействий динамику проходящих в этих средах потоков.
Если финансовый рынок обладает свойствами нелинейной динамической системы, то возникает вполне логичный вопрос – можно ли теорию нелинейных динамических систем применить к описанию и моделированию динамики финансового рынка? Ответ утвердительный – да, можно!
Вспомним определение понятия “Финансы”.
Финансы – это совокупность экономических отношений, возникающих в процессе формирования, распределения и использования централизованных и децентрализованных фондов денежных средств.
Из определения следует, что финансы – это движение денежных средств, то есть финансы – это динамика.
Экономическая система аналогична физической системе, и там и там присутствуют потоки частиц. В физической системе такими частицами могут быть частицы газа, воды, плазмы, а в экономической системе такими частицами можно считать денежные средства во всех их формах и проявлениях.
Внешнее воздействие на физическую систему, например, изменение таких параметров как температуры, давления или того и другого, приводит к изменению в этой системе динамики потоков. Аналогично можно говорить и об экономической системе, где под внешними воздействиями, например, такими как, изменение процентной ставки, величин спроса и предложения, нормы прибыли в какой-нибудь отрасли и др., происходит изменение динамики денежных потоков, которые меняют направления перемещаясь как внутри и вне локального рынка, так и между другими различными рынками – валютными, фондовыми, товарными, сырьевыми, то есть внутри всеобъемлющего финансового рынка.
Финансовые рынки представляют собой потоки денежных средств в экономике и эти потоки денежных средств не являются равномерными, их можно характеризовать как турбулентные и хаотические по аналогии с потоками, образующимися в различных физических системах.
Генератором простейшего денежного потока является человек как субъект экономических отношений, на которого воздействует окружающая его среда, включающая информационное поле.
Каждый человек располагает некоторой денежной суммой, пришедшей ему в виде зарплаты, пособия, дивидендов, процентов и прочих доходов от источников, которых не перечислить. Тратя свои средства, человек, сам того не осознавая, формирует определённые денежные потоки. Эти денежные потоки людей по отдельности малозаметны и не ощутимы, они подобны каплям воды, из которых сформированные тонкие струйки вливаются в ручейки, затем с ручейками в реки, из рек в моря и дальше в океаны с последующими испарениями и превращениями опять в капли.
Денежные потоки, формируемые сотнями, тысячами, миллионами людей уже становятся заметными и ощутимыми. Например, спрос на продукцию компании Apple сформировал денежные потоки колоссальных объёмов, сумевших резко поднять рыночную капитализацию этой компании.
В общем, финансовый рынок представляет собой нелинейную динамическую систему с неравномерными денежными потоками, а значит для описания динамики финансового рынка можно применять весь инструментарий, который только применим к нелинейным динамическим системам.
В физических системах количество внешних воздействий является конечным числом. Если говорить языком математики, то под внешним воздействием понимается некая переменная. С конечным числом переменных можно вводить понятие функции, описывающей зависимость динамики потока от изменения этих переменных, а саму зависимость выражать через уравнение, имеющее конечное число решений.
Например, наличие в физической системе двух внешних на неё воздействий в виде температуры и давления позволяет представить скорость изменения потока как функцию от этих двух переменных.
Но экономическая система – это далеко не физическая система, в которой можно бесконечное число раз ставить эксперименты, меняя параметры внешних воздействий и в конце привести эту систему в исходное состояние.
Финансовый рынок – это система количество внешних воздействий на которую не имеет конечного числа. Внешним воздействием может быть абсолютно всё – от учётной ставки до непроверенных слухов.
Можно говорить, что стоимость на финансовом рынке есть функция от бесконечного числа внешних воздействий, являющихся независимыми переменными:
P = F(x1, x2, x3, …, xn)
где
P – цена финансового актива;
Xn – внешнее воздействие, n→∞.
Решение этого уравнения, т.е. нахождение величины будущей стоимости финансового актива, в такой постановке задачи не представляется возможным.
Нужен другой подход.
Вспомним, что решение квадратного уравнения можно найти не только по формулам из уравнения функции, но и по графику этой функции.
Подход, при котором решение уравнения может быть найдено графическим способом, применим и к нелинейным динамическим системам.
Для этого сделаем несколько допущений.
Денежные потоки выражаются в стоимостных величинах. Так, динамика денежных потоков между хозяйствующими субъектами находит своё отражение в финансовых отчётах этих субъектов, ну а в более глобальном масштабе – в торговых балансах стран. Динамика же денежных потоков на финансовом рынке находит своё отражение в динамике стоимости финансовых активов.
Организованные рынки (биржи, электронные торговые площадки), в совокупности с информационными технологиями, дают нам уникальную возможность в режиме реального времени наблюдать за динамикой денежных потоков на валютном, фондовом, товарном, сырьевом рынках, как в отдельно взятом регионе, так и в глобальном Мире.
Рассмотрим механизм формирования цен финансовых инструментов на организованном рынке.
Инвесторы, желающие что-то купить или что-то продать, выставляют соответствующие заявки на покупку или продажу тех или иных финансовых активов.
Объёмы заявок, выставленных на покупку по конкретной цене, превышающие объёмы заявок, выставленных на продажу по той же цене, в определённый момент времени двигают цену этого финансового актива вверх. И наоборот, объёмы заявок, выставленных на продажу по конкретной цене, превышающие объёмы заявок, выставленных на покупку по той же цене, в определённый момент времени двигают цену финансового актива вниз.
Таким образом, можно говорить, что на цену финансового актива влияет только один единственный фактор, а именно – ордера, выставляемые инвесторами в стакан. Только лишь выставленные и исполненные ордера двигают цены вниз или вверх.
В таком случае, все организованные рынки, включающие в себя всех участников процесса – от регуляторов и организаторов торгов до покупателей и продавцов, на которых торгуются финансовые инструменты, условно можно считать некими чёрными ящиками, на выходе из которых посредством стакана, как некоего измерительного прибора, фиксируются показания котировок в каждый конкретный момент времени. Нанесённые на график показания из стакана будут описывать динамику денежных потоков.
Максимально всё упрощая, график изменения стоимости во времени, можно представить, как график функции N, которая является оператором, задающим соответствие между множеством значений P и множеством значений T:
P = N(T)
где
P – цена финансового актива;
T – время.
С учётом того, что это график нелинейной функции, описывающей динамику нелинейной динамической системы, можно говорить о том, что график является аттрактором, структура которого формируется динамическими фракталами.
Чтобы двигаться дальше, необходимо освежить в памяти некоторые понятия и их определения.
Динамическая система.
Под динамической системой понимается процесс, для которого однозначно определено понятие состояния как совокупности значений некоторых величин в заданный момент времени и задан оператор, определяющий эволюцию начального состояния во времени.
Аттрактор.
Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться периодическая траектория или некоторая ограниченная область с неустойчивыми траекториями внутри в случае странного аттрактора.
Странный аттрактор.
Особенность странного аттрактора заключается в его масштабной инвариантности, выражающейся в том, что при увеличении или уменьшении масштаба некоторой подобласти странного аттрактора получается геометрический объект, сходный по своей структуре с целым аттрактором.
Фазовое пространство.
Фазовое пространство системы — это совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из одного состояния в другое.
Точка бифуркации.
Точка бифуркации — критическое состояние динамической системы, при котором система становится неустойчивой относительно флуктуаций в ней происходящих и возникает неопределенность: останется ли состояние системы хаотическим или она перейдет на новый, более высокий уровень упорядоченности.
Хаос.
Хаос – это неповторяющаяся, нерегулярная, беспорядочная последовательность состояний динамической системы или беспорядочное поведение аттракторов этой системы.
Фрактал.
Фракталом называется структура, состоящая из частей, которые подобны целому. Также можно сказать, что фрактал является аттрактором нелинейной динамической системы.
Динамический фрактал.
Динамические фракталы описывают динамику процессов, протекающих во времени в нелинейных динамических системах. В своём развитии нелинейная динамическая система проходит через чередующиеся этапы устойчивого и хаотического состояния в результате чего из хаоса возникают упорядоченные состояния, приводящие систему обратно в хаотическое состояние.
Синергетика.
Синергетика (от греч. synergeia — сотрудничество, содействие, соучастие) — междисциплинарное направление научных исследований, в рамках которого изучаются общие закономерности процессов перехода от хаоса к порядку и обратно (процессов самоорганизации и самопроизвольной дезорганизации) в открытых нелинейных системах физической, химической, биологической, экологической, социальной и др. природы.
Суть подхода синергетики к описанию динамики финансового рынка заключается в том, что сложноорганизованные системы, состоящие из большого количества элементов, находящихся в сложных взаимодействиях друг с другом и обладающих огромным числом степеней свободы, могут быть описаны небольшим числом существенных типов движения (параметров порядка), а все прочие типы движения оказываются подчиненными и могут быть достаточно точно выражены через параметры порядка. Поэтому сложное поведение систем, таких как финансовый рынок, может быть описано при помощи иерархии упрощенных моделей, включающих небольшое число наиболее существенных степеней свободы.
3.2. Финансовый рынок – это НДАСС.
Финансовый рынок – это нелинейная динамическая система. Именно нелинейная парадигма даёт возможность понять и описать динамику финансового рынка, используя соответствующий математический инструментарий для нелинейных динамических аддитивно-синергетических систем (НДАСС).
В основе метода моделирования динамики котировок финансовых инструментов лежат:
- теория хаоса;
- фрактальная геометрия;
- синергетика.
3.3. Стоимость есть функция времени: P = N(T).
Отталкиваясь от того, что финансовый рынок представляет собой нелинейную динамическую систему, график изменения стоимости финансового актива от времени можно рассматривать как график функции N, которая является оператором, задающим соответствие между множеством значений P и множеством значений T:
P = N(T)
где
P – цена финансового актива;
T – время.
С учётом того, что это график нелинейной функции, описывающей динамику нелинейной динамической системы, можно говорить о том, что этот график является аттрактором, структура которого формируется динамическими фракталами.
3.4. Фрактал и фрактальная структура.
Метод моделирования динамики стоимости финансового актива построен на анализе аттрактора оператора N формирующего его фрактальную структуру, которая даёт понимание того, какие фракталы сформировались, какие фракталы формируются и как следствие – какие фракталы будут формироваться, тем самым показывая будущие направления возможной динамики его стоимости.
Введём определение фрактала и фрактальной структуры.
Под фракталом будем понимать простейший аттрактор колебательного движения, состоящий из трёх сегментов, из которых один (2-ой сегмент) направлен в противоположную сторону двум другим (1-ому и 3-ему сегментам).
Фракталы разделяются на виды и типы в зависимости от размеров стоимостных и временных интервалов своих сегментов.
Согласно свойству самоподобия фракталы меньшего порядка формируют фракталы большего порядка, соответственно фракталы большего порядка состоят из фракталов меньшего порядка.
3.5. Порядок, виды и типы фракталов.
Таким образом, любой фрактал помимо стоимостных и временных значений интервалов имеет следующие описывающие его характеристики:
1. Порядок фрактала, указывающий каким сегментом он является по отношению к фракталам большего порядка и какими сегментами фракталов меньшего порядка он сформирован сам.
2. Тип фрактала.
3. Вид фрактала.
Фрактальная структура, в таком случае, – это взаимосвязь фракталов различных порядков, видов, типов между собой.
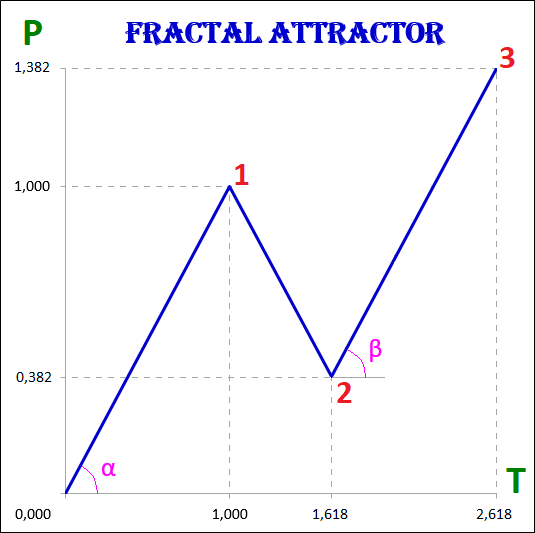
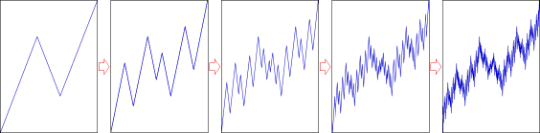
3.8. Динамика базисного фрактала.
В данном примере все сегменты фракталов – и первые, и вторые, и третьи, вне зависимости от их порядка – первого, второго, третьего, четвёртого или пятого, имеют стоимостные и временные интервалы базисного фрактал-аттрактора, а именно:
1) Р1 = Р3 и Т1 = Т3;
2) Р2 / Р1 = Т2 / Т1 = 0,618.
3.9. Описание фрактальной структуры.
Реальная рыночная динамика стоимости любого финансового актива описывается оператором N.
Базисный фрактал – это один из множества фракталов, которые формируют фрактальную структуру графиков динамики стоимости, представляющих собой аттракторы.
Описать фрактальную структуру аттрактора – значит описать типы и виды фракталов её составляющих, их последовательность и расположение по отношению друг к другу.
Фрактальная структура аттрактора одновременно и настолько сложна, и настолько проста, что невозможно сказать, чего же на графике котировок финансовых активов больше – хаоса или порядка.
Сначала дадим определение хаоса и порядка во фрактальной структуре, затем опишем обозначение фракталов во фрактальной структуре после чего приведём их классификацию по видам и типам.
3.10. Определение порядка и хаоса.
Порядок – это завершённый фрактал.
Завершённым считается фрактал, у которого сформированы все три его сегмента – 1ый, 2-ой и 3-ий. Завершение 3-го сегмента говорит о завершении всего фрактала, так как этому предшествует последовательное завершение 1-го и 2-го сегментов.
Хаос в таком случае – это процесс формирования фрактала.
Другими словами, порядок дискретен, а хаос непрерывен. Завершение 3-го сегмента одного фрактала сменяется началом 1-го сегмента другого фрактала того же порядка или выше.
С учётом того, что фракталы меньшего порядка формируют фракталы большего порядка, можно говорить о том, что хаос и порядок не разделимы.
Порядок присутствует в хаосе и хаос присутствует в порядке. Хаос и порядок пронизывают друг друга и существуют один в другом.
Динамику стоимости на финансовом рынке можно характеризовать и как хаотическую, и как упорядоченную. Но сам хаос есть не что иное как порядок наивысшего уровня, потому что ничего хаотического не происходит, так как график этой динамики является аттрактором динамического фрактала, определяемого оператором N.
3.11. Порядок фракталов.
Каждый фрактал является первым, вторым или третьим сегментом другого фрактала, который имеет больший порядок.
Для точного описания местоположения фракталов во фрактальной структуре требуется их обозначение, присвоение фракталам неких номеров, позволяющих однозначно понимать, какими сегментами являются фракталы и каков их порядок по отношению к другим фракталам.
Фрактал, номер которого состоит из одной цифры, является фракталом 1-го порядка, являющегося наивысшим.
Фрактал, номер которого состоит из двух цифр, является фракталом 2-го порядка, из трёх – 3-го порядка, из четырёх – 4-го и т.д.
Фракталы 4-го порядка составляют фракталы 3-го порядка, которые в свою очередь составляют фракталы 2-го порядка, а те уже составляют фракталы наивысшего 1-го порядка.
3.12. Нумерация фракталов.
Фрактал наивысшего 1-го порядка имеет номер 1, 2 или 3 в соответствии с тем, каким сегментом он является – первым, вторым или третьим. Фрактал 1-го порядка состоит из сегментов, которые являются фракталами 2-го порядка.
Фрактал с номером 1 состоит из сегментов с номерами: 11 (1-ый сегмент), 12 (2-ой сегмент) и 13 (3-ий сегмент).
Фрактал с номером 2 состоит из сегментов с номерами: 21 (1-ый сегмент), 22 (2-ой сегмент) и 23 (3-ий сегмент).
Фрактал с номером 3 состоит из сегментов с номерами: 31 (1-ый сегмент), 32 (2-ой сегмент) и 33 (3-ий сегмент).
Фракталы имеют один порядок если они либо являются сегментами одного фрактала, его составляющего, либо являются сегментами других фракталов, которые в свою очередь являются сегментами другого фрактала.
Фрактал имеет на один порядок меньше чем другой фрактал, если он является его сегментом.
Фрактал имеет на один порядок больше чем другой фрактал, если тот другой фрактал является его сегментом.
Фрактал, обозначенный номером, подобен точке, обозначенной координатами, которую легко найти в соответствующей системе координат. В нашем случае системой координат является фрактальная структура.
Так, например, если координатами фрактала является номер 132, то это означает, что данный фрактал является 2-ым сегментом фрактала 2-го порядка с номером 13, который в свою очередь является 3-им сегментом фрактала 1-го порядка с номером 1.
3.13. Определение точек экстремумов.
Динамика стоимости на финансовом рынке – это чередование трендов на повышение и трендов на понижение с образованием на графиках точек локальных и глобальных экстремумов.
С точки зрения фрактальной структуры графиков точки экстремумов (точки где сменяются тренды) представляют собой точки в которых завершают своё формирование одни сегменты фракталов и начинают формироваться другие.
3.14. Виды и типы фракталов.
У фрактала три сегмента – первый, второй и третий. Второй сегмент фрактала всегда направлен в противоположную сторону первому и третьему сегментам.
Помимо порядка, обозначающего также и номер сегмента, каждый сегмент фрактала имеет две характеристики (два параметра) – это цена Р (стоимостной интервал) и время Т (временной интервал).
P – это стоимостная характеристика, показывающая длину проекции сегмента фрактала на ценовую ось, тем самым обозначая ценовой интервал, в котором сформировался сегмент.
Т – это временная характеристика, показывающая длину проекции сегмента фрактала на ось времени, тем самым обозначая временной интервал, который потребовался для формирования сегмента.
Фрактал, состоящий из трёх сегментов, имеет шесть характеристик – это P1, Р2, Р3, Т1, Т2, Т3:
• Р1 и Т1 – ценовой и временной интервалы 1-го сегмента;
• Р2 и Т2 – ценовой и временной интервалы 2-го сегмента;
• Р3 и Т3 – ценовой и временной интервалы 3-го сегмента.
Основным фракталом является базисный фрактал, стоимостные и временные параметры сегментов которого соотносятся между собой в следующих пропорциях:
1-ая пропорция:
Р1/Р3 = Т1/Т3 = 1;
2-ая пропорция:
Р2/Р1 = Т2/Т1 = 0,618.
Изменяя при помощи золотого сечения значения параметров базисного фрактала используя коэффициенты Фибоначчи, получим некоторое множество фракталов, которое можно классифицировать по видам и типам.
Из соотношения стоимостных параметров 1-го и 3-го сегментов можно выделить три вида фракталов.
Вид №1 – это фракталы, у которых ценовой интервал третьего сегмента больше ценового интервала первого сегмента:
Р1 < Р3;
Вид №2 – это фракталы, у которых ценовой интервал третьего сегмента равен ценовому интервалу первого сегмента:
Р1 = Р3;
Вид №3 – это фракталы, у которых ценовой интервал третьего сегмента меньше ценового интервала первого сегмента:
Р1 > Р3.
Относительно каждого вида фракталов можно сказать, что 2-ой вид фракталов характеризует нормальную динамику, 1-ый вид фракталов характеризует динамику с ускорением, а 3-ий вид фракталов характеризует динамику с торможением.
Из соотношений стоимостных и временных параметров 1-го, 2-го и 3-го сегментов между собой можно выделить пять типов фракталов в каждом виде.
Три вида и пять типов дают 15 фракталов, включая базисный.
Фракталы 1-ого вида обозначаются следующими номерами:
11, 12, 13, 14, 15.
Фракталы 2-ого вида обозначаются следующими номерами:
21, 22, 23, 24, 25.
Фракталы 3-его вида обозначаются следующими номерами:
31, 32, 33, 34, 35.
Первая цифра в номере указывает на вид фрактала – 1ый, 2-ой или 3-ий, а вторая цифра в номере указывает на тип фрактала – 1-ый, 2-ой, 3-ий, 4-ый или 5-ый.
Рассмотрим каждый из 15 фракталов по отдельности и обозначим пропорции между величинами стоимостных и временных интервалов сегментов их составляющих.
Начнём рассмотрение с фракталов 1-го вида, продолжим фракталами 2-го вида и завершим фракталами 3-го вида.
3.15. 15 фракталов:
3.15.1. Фракталы 1-го вида.
Фракталы 1-го вида имеют следующие номера: 11, 12, 13, 14, 15.
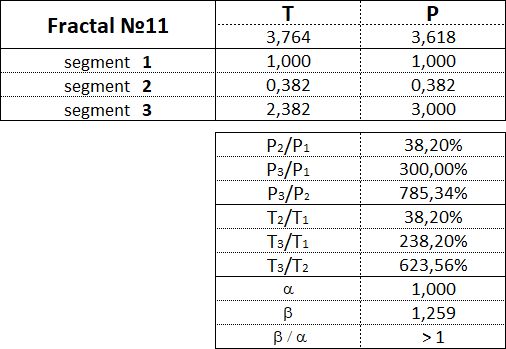
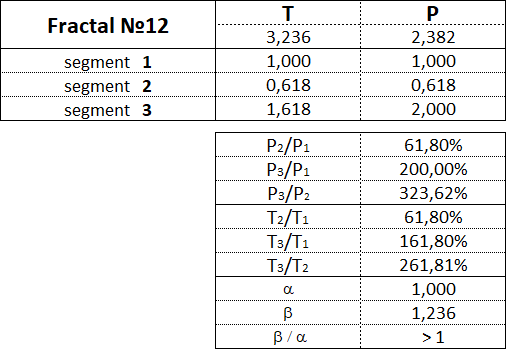
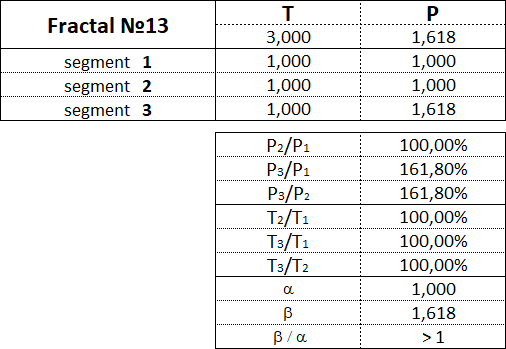
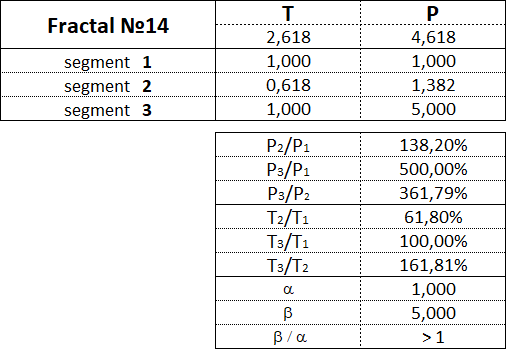
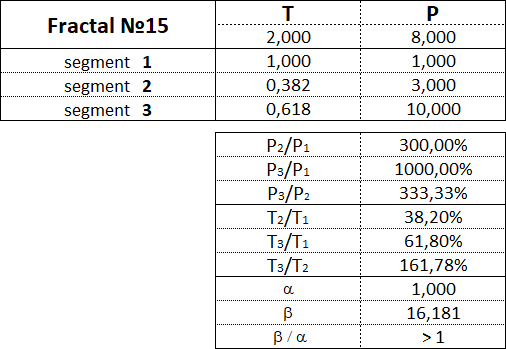
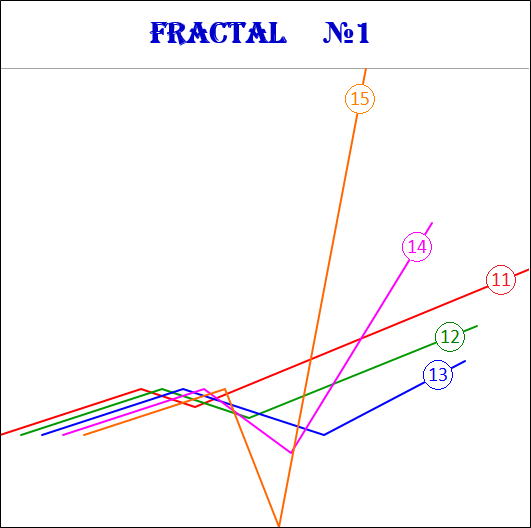
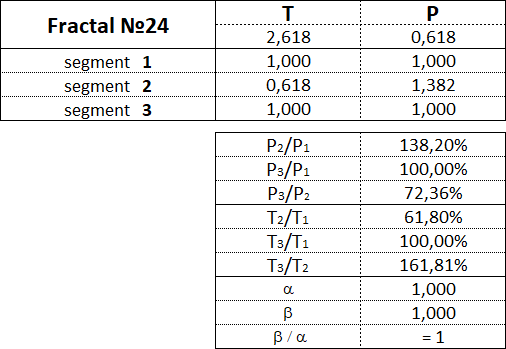
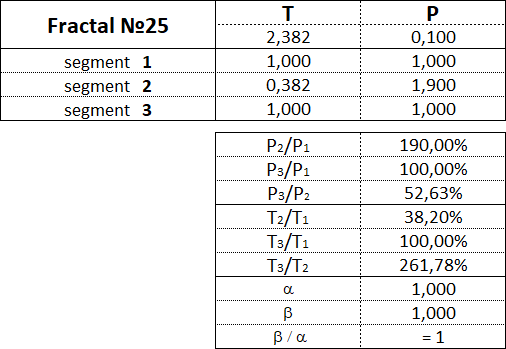
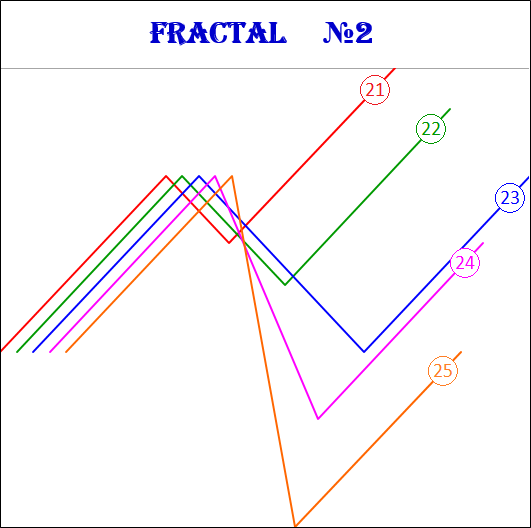
3.15.2. Фракталы 2-го вида.
Фракталы 2-го вида имеют следующие номера: 21, 22, 23, 24, 25.
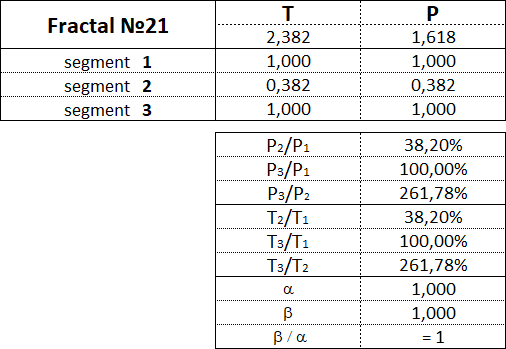
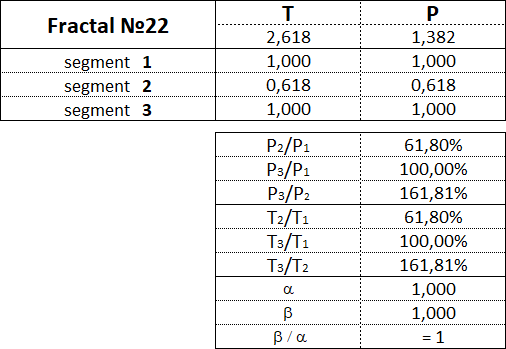
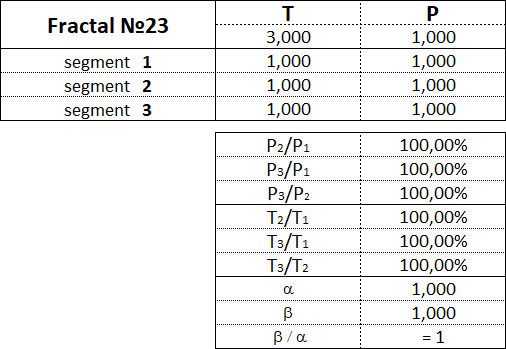
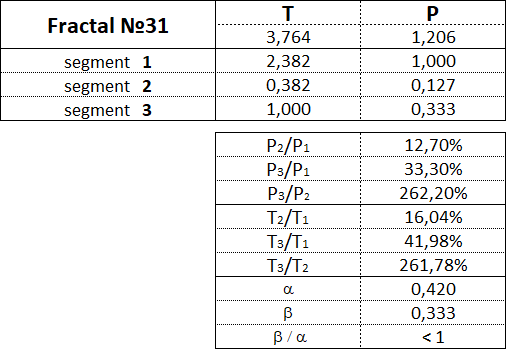
3.15.3. Фракталы 3-го вида.
Фракталы 3-го вида имеют следующие номера: 31, 32, 33, 34, 35.
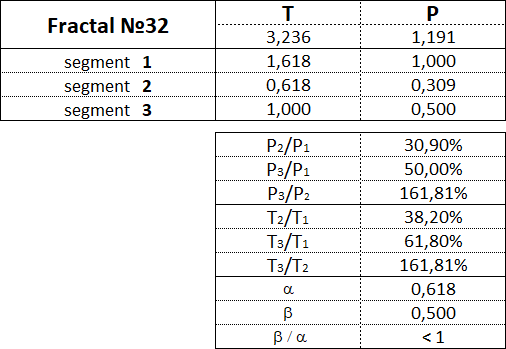
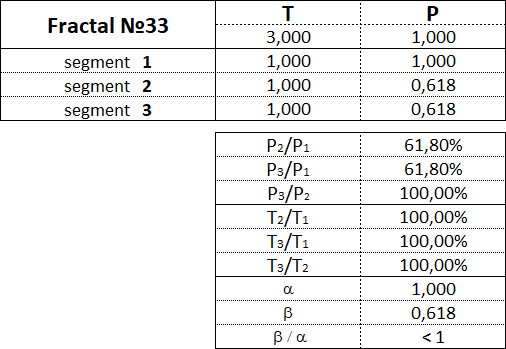
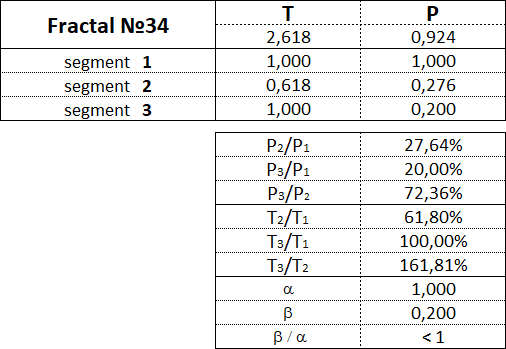
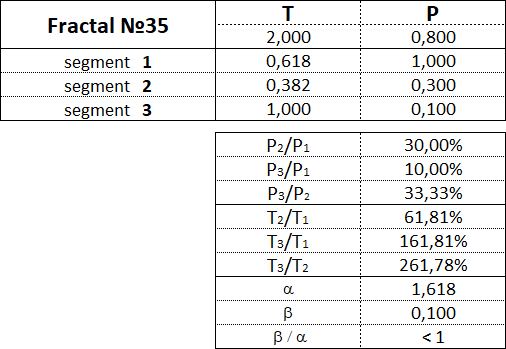
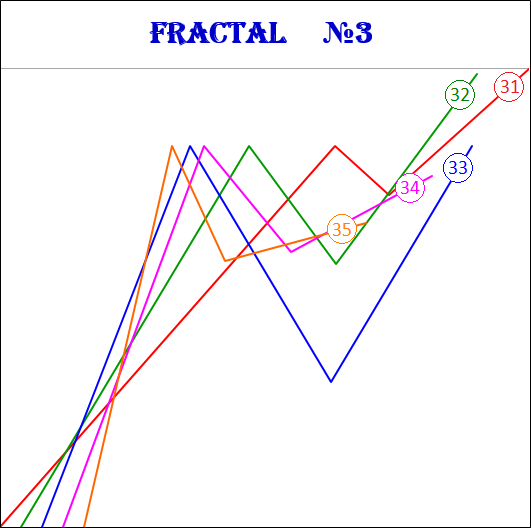
3.16. Пропорции между сегментами фракталов.
В данной таблице приведены диапазоны значений в процентном отношении между стоимостными и временными параметрами сегментов для каждого из 15 фракталов.
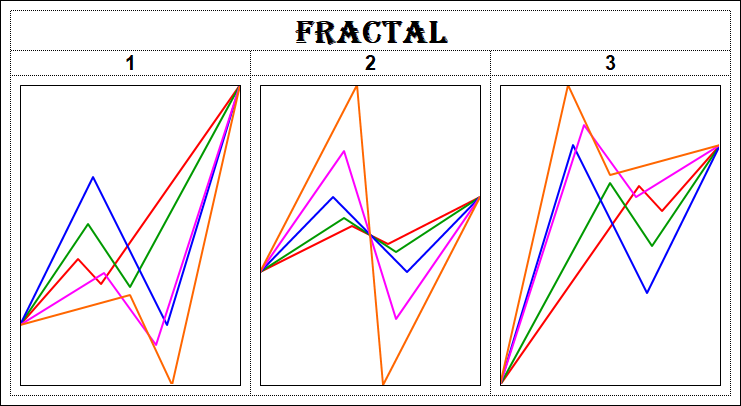
3.17. Азбука аттракторов Niro.
Из 15 фракталов можно составить некое подобие алфавита из 15 букв.
Как в азбуке Морзе, комбинациями двух символов – точек и тире, можно написать любой текст, так и в азбуке аттракторов Niro комбинациями 15 фракталов можно описать любую фрактальную структуру FS любого базисного актива BA.
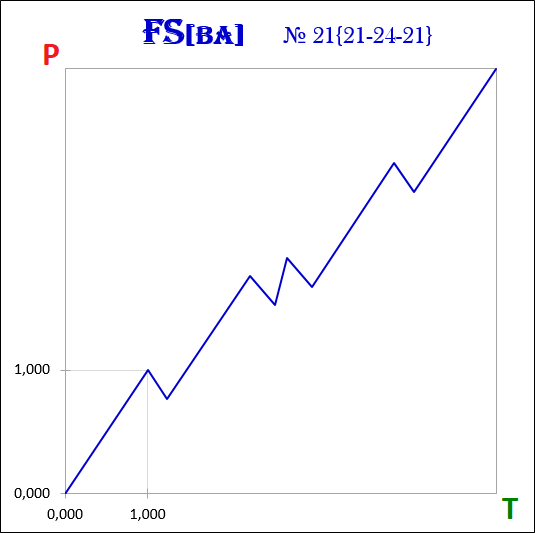
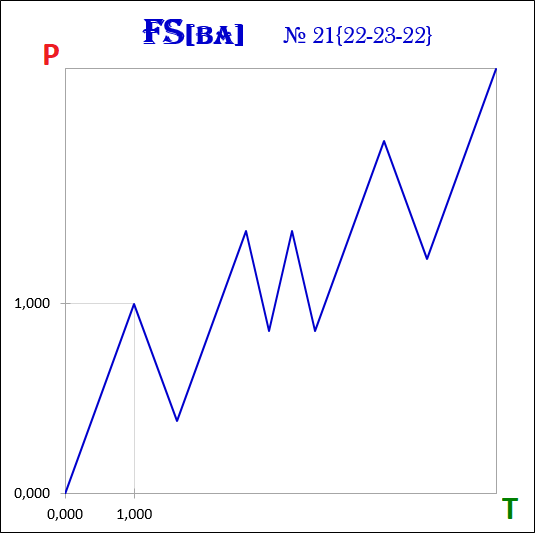
3.18. Точка бифуркации и степени свободы.
Нелинейная динамическая система пребывает в хаосе до тех пор, пока во фрактальной структуре графика не будет сформирован фрактал. Сформированный фрактал означает, что система из хаотического состояния перешла в упорядоченное состояние. Порядок, возникший из хаоса, будет нарушен началом формирования нового фрактала в противоположном направлении уже сформированному и система обратно вернётся в хаотическое состояние.
Нелинейная динамическая система в момент завершения фрактала находится в точке бифуркации, в которой у системы появляется несколько степеней свободы – несколько вариантов дальнейшего развития её фрактальной структуры. В точке бифуркации однозначно можно говорить только лишь о смене тренда, то есть смене направления будущего фрактала на противоположное завершившемуся фракталу, всё остальное – стоимостные и временные интервалы будущих фракталов, остаётся неясным, неподлежащим однозначному определению.
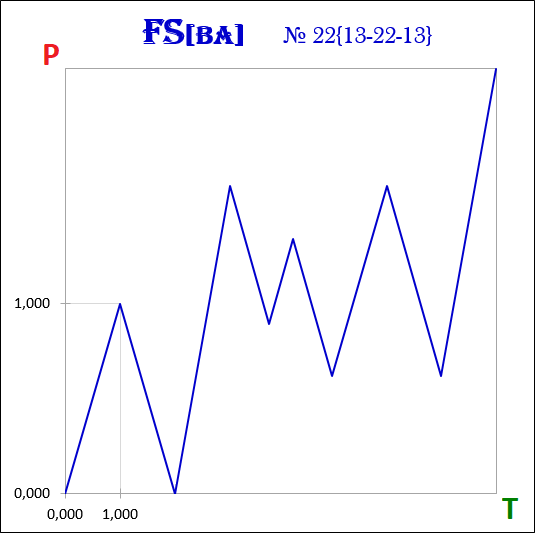
Рассмотрим пример формирования фрактальной структуры нелинейной динамической системы с двумя степенями свободы в точках бифуркации для трёх временных интервалов. Под временным интервалом понимается период времени, который необходим для формирования фракталов одинакового порядка.
1-ый сценарий развития – это сценарий, при котором стоимостной интервал нового фрактала не превышает стоимостного интервала завершившегося фрактала.
2-ой сценарий развития – это сценарий, при котором стоимостной интервал нового фрактала превышает стоимостной интервал завершившегося фрактала.
Обозначим через Т0 интервал времени, за который был сформирован начальный фрактал.
Тогда в интервале Т1 могут быть сформированы два фрактала, в интервале Т2 – четыре фрактала, а в интервале Т3 – восемь фракталов.
Число степеней свободы в точках бифуркации нелинейной динамической системы определяет количество возможных сценариев развития её фрактальной структуры в текущем временном интервале, которое с каждым последующим временным интервалом будет увеличиваться в геометрической прогрессии.
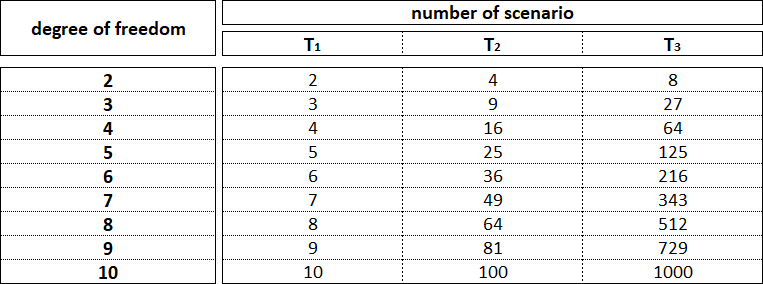
Число степеней свободы в точке бифуркации нелинейной динамической системы величина не постоянная и зависит от её местоположения во фрактальной структуре.
Минимальное число степеней свободы нелинейная динамическая система имеет тогда, когда точка бифуркации во фрактальной структуре находится в начале формирования фрактала наименьшего порядка, который завершает фрактал наибольшего порядка.
Максимальное число степеней свободы приходится на точку бифуркации, которая разделяет завершение фрактала наибольшего порядка и начало фрактала наименьшего порядка.
С учётом этого моделирование фрактальной структуры нелинейной динамической системы далее второго временного интервала не имеет никакого практического смысла из-за наличия большого количества возможных сценариев развития фрактальной структуры.
3.19. Стоимостные и временные интервалы.
Фрактальная структура аттрактора формируется динамическими фракталами различного порядка. В любой момент времени все фракталы, которые формируют фрактальную структуру, находятся на разной стадии своего завершения – фракталы одних порядков могут быть полностью завершёнными, других порядков – находиться в начальной стадии своего формирования, третьих порядков – в конечной, а четвёртых – в промежуточной.
Завершённый, т.е. сформированный, фрактал – это фрактал, у которого последовательно завершены все три его сегмента. Завершение 3-го сегмента фрактала – это завершение всего фрактала целиком.
Завершение фрактала означает завершение стоимостных и временных интервалов его сегментов.
Стоимостной интервал фрактала – это интервал между началом проекции на ценовую ось 1-го сегмента фрактала и концом проекции 3-го его сегмента.
Временной интервал фрактала – это интервал между началом проекции на ось времени 1-го сегмента фрактала и концом проекции 3-го его сегмента. Временной интервал фрактала есть сумма временных интервалов всех трёх его сегментов.
Струнами фрактальной структуры аттрактора называются горизонтальные уровни, которые проведены через точки экстремумов, сформированные в каждом месяце. Количество струн фрактальной структуры равно удвоенному количеству месяцев, потребовавшихся на её формирование.
В подавляющем большинстве случаев начало и окончание стоимостных интервалов будут находиться в окрестностях точек, лежащих на струнах.
Длина стоимостного интервала является величиной абсолютной, а длина временного интервала – величиной относительной.
Время есть форма протекания процесса формирования фрактальной структуры и условие возможности её изменения.
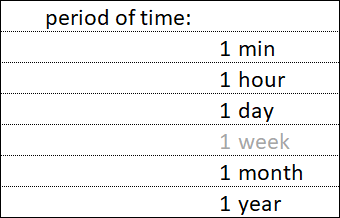
Все эти простые периоды, кроме недельного, кратны друг-другу. Так в годовом периоде содержится целое число месячных периодов, в месячном периоде содержится целое число дневных периодов, в дневном периоде содержится целое число часовых периодов, в часовом периоде содержится целое число минутных периодов.
Временные интервалы сформированных фракталов расположены относительно простых периодов времени неравномерно, но с определённой закономерностью.
Начало и конец временного интервала может совпадать с началом и концом простого периода времени, но в подавляющем большинстве случаев начало и конец временных интервалов приходятся на окрестности точек, которые делят простые периоды времени по золотому сечению с коэффициентами Фибоначчи 0,382 и 0,618.
Чтобы фрактальную структуру графика раскладывать на отдельные фракталы с тремя сегментами, недостаточно анализировать графики, которые построены по простым временным периодам – 1 минута, 1 час, 1 день, 1 месяц, 1 год. Для нахождения фрактальной структуры требуется анализировать графики, которые построены по всем возможным тайм-фреймам.
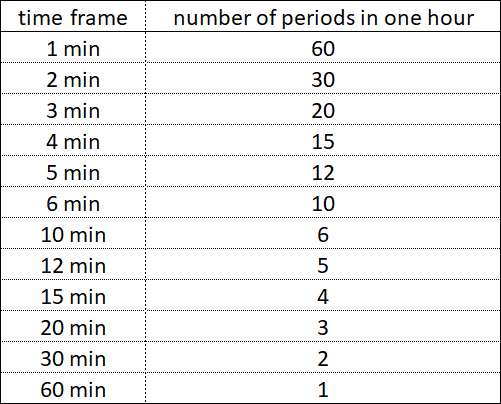
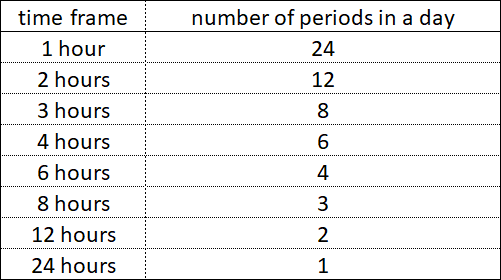
Внутри каждого простого периода времени – будь то 1 час, 1 день или 1 год имеются, более мелкие временные периоды, их составляющие, которые завершаются одновременно друг с другом на определённых временных отрезках.
Внутри 1 часа периоды с тайм-фреймами 30 минут, 20 минут, 12 минут одновременно не завершаются, а вот периоды с тайм-фреймами 30 минут, 15 минут, 5 минут на некоторых временных отрезках завершаются одновременно.
Внутри 1 дня периоды с тайм-фреймами 8 часов и 6 часов одновременно не завершаются, а вот периоды с тайм-фреймами 8 часов, 4 часа, 2 часа или 12 часов, 6 часов и 3 часа на некоторых временных отрезках завершаются одновременно.
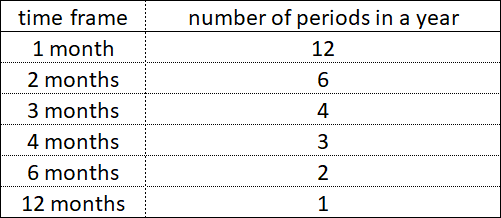
Внутри 1 года периоды с тайм-фреймами 4 месяца и 3 месяца одновременно не завершаются, а вот периоды с тайм-фреймами 6 месяцев и 2 месяца на некоторых временных отрезках завершаются одновременно.
Периоды всех тайм-фреймов, одновременно начавшись, также одновременно завершаются в конце простого периода времени.
Фракталы низких порядков формируют фрактальные структуры на временных интервалах с дневными тайм-фреймами, а на временных интервалах с часовыми тайм-фреймами формируются фрактальные структуры фракталами ещё более низших порядков.
Фракталы высших порядков формируют фрактальные структуры на временных интервалах с месячными тайм-фреймами, а фракталы наивысших порядков формируют фрактальные структуры на временных интервалах с годовыми тайм-фреймами.
Завершения стоимостных и временных интервалов происходят в точках бифуркации, находящихся в подавляющем большинстве случаев на струнах фрактальных структур. С учётом наличия в точках бифуркации у нелинейной динамической системы большого количества степеней свободы моделирование будущей фрактальной структуры далее вторых стоимостных и временных интервалов приводит к огромному количеству моделей, зачастую имеющих одинаковую вероятность реализации, что не позволяет выбрать одну единственную модель как на наиболее вероятную для реализации.
Более точное прогнозирование будущей динамики стоимости финансовых инструментов достигается анализом и моделированием фрактальной структуры их графиков между двумя ближайшими друг к другу точками бифуркаций, т.е. только лишь в текущем стоимостном и временном интервалах – в направлении формирования либо 1-го сегмента, либо 2-го сегмента, либо 3-го сегмента фрактала.
Для краткосрочного прогнозирования динамики стоимости финансовых инструментов необходимо проводить моделирование фрактальной структуры графиков, которые построены по минутным и часовым тайм-фреймам.
Для среднесрочного прогнозирования динамики стоимости финансовых инструментов необходимо проводить моделирование фрактальной структуры графиков, которые построены по дневным и недельным тайм-фреймам.
Для долгосрочного прогнозирования динамики стоимости финансовых инструментов необходимо проводить моделирование фрактальной структуры графиков, которые построены по месячным и годовым тайм-фреймам.
Горизонт прогнозирования во всех трёх вариантах будет одним и тем же – текущий стоимостной и текущий временной интервалы формирующегося фрактала, т.е. формирующихся его первого, второго или третьего сегментов.
Вот только на графиках с часовыми тайм-фреймами горизонтом прогнозирования будет период в несколько дней или недель, на графиках с дневными и недельными тайм-фреймами горизонтом прогнозирования будет период в несколько месяцев, ну а на графиках с месячными и годовыми тайм-фреймами горизонтом прогнозирования уже будет период в несколько лет и даже десятилетий.
Стоимостные интервалы фракталов вне зависимости от их порядка стремятся к завершению в точках, которые находятся либо в точках, лежащих на струнах фрактальной структуры, либо в точках, находящихся на удалении от струн в соответствии с коэффициентами Фибоначчи.
Временные интервалы фракталов, порядок которых ниже высшего, стремятся к завершению в окрестностях концевых точек временных отрезков, которые расположены внутри простых временных периодов в соответствии с коэффициентами Фибоначчи.
Наложение точек окончаний стоимостных и временных интервалов фракталов образуют точки бифуркаций, которые предопределяют величины будущих стоимостных и временных интервалов новых фракталов.
Прогнозирование динамики стоимости на долгосрочный период требует проведения анализа фрактальных структур, сформированных фракталами высшего и наивысшего порядков, образование точек бифуркации в которых отлично от фрактальных структур, образованных фракталами порядка ниже наивысшего.
Завершение временных интервалов фракталов высшего и наивысшего порядков происходит в окрестностях точек, в которых происходит одновременное окончание максимального количества годовых тайм-фреймов:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 и 34,
Особое внимание требуется уделять одновременному окончанию годовых тайм-фреймов, среди которых присутствуют тайм-фреймы Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34.
На временном интервале от 1-го года до 40-го максимальное количество одновременных окончаний тайм-фреймов равно 8.
По 8 одновременных окончаний происходит в 24-ом, 30-ом и 36-ом годах.
В 24-ом году одновременно оканчиваются следующие годовые тайм-фреймы:
1, 2, 3, 4, 6, 8, 12, 24.
В 30-ом году одновременно оканчиваются следующие годовые тайм-фреймы:
1, 2, 3, 5, 6, 10, 15, 30.
В 36-ом году одновременно оканчиваются следующие годовые тайм-фреймы:
1, 2, 3, 4, 6, 9, 12, 18.
На временном отрезке с 1 по 2200 год количество одновременных завершений тайм-фреймов в годах с 1 по 34 варьируется от 1 до 18.
18 – это максимальное количество одновременных завершений на этом временном отрезке, которое приходится на 1680 год. В этом году одновременно завершаются следующие тайм-фреймы: 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 16, 20, 21, 24, 28, 30.
Количество одновременных завершений тайм-фреймов на интервале (1; 2200) от 1 до 9 составляет 93,09%, остальные 6,91% приходится на количество одновременных завершений от 10 до 18.
Окончание временных интервалов фракталов наивысшего порядка происходит на временных отрезках, где количество одновременных завершений тайм-фреймов принимает значения от 10 до 18.
Сводные данные об одновременных завершениях тайм-фреймов в годах с 1 по 34 за период с 1 по 2200 год приведены ниже на графике и в таблице.
При анализе временных интервалов фракталов наивысших порядков незавершённый год округляется до завершённого, что не позволяет делать анализ более точным.
Чтобы сделать анализ временных интервалов c точностью до месяца, необходимо построить по аналогии с годовыми тайм-фреймами месячные тайм-фреймы с 1 по 34 за период с 1 года по 2100 год и найти временные отрезки, в которых одновременно завершается максимальное количество периодов с разными месячными тайм-фреймами.
В таком случае декабрь 2000 года будет 24000 месяц, декабрь 2100 года будет 25200 месяц, а июль 2021 года – это 24247 месяц.
Временной интервал 1-2100 год содержит 25’200 месяцев. На этом временном интервале количество одновременных завершений тайм-фреймов в месяцах с 1 по 34 варьируется от 1 до 21 (21/34=0,618 – “золотое сечение”).
21 – это максимальное количество одновременных завершений на этом временном интервале, которое приходится на следующие года: 840, 1260, 1540, 1680 и 2100 годы.
Количество одновременных завершений тайм-фреймов на интервале (1; 25’200) от 1 до 9 составляет 92,96%, остальные 7,04% приходится на количество одновременных завершений от 10 до 21.
Окончание временных интервалов фракталов наивысшего порядка происходит на временных отрезках, где количество одновременных завершений тайм-фреймов принимает значения от 10 до 21.
Сводные данные об одновременных завершениях тайм-фреймов в месяцах с 1 по 34 на интервале за период с 1 по 2100 год приведены ниже на графике и в таблице.
Обозначим временной интервал как (1; L). где L ∈ N.
ТF – тайм-фрейм, период времени, повторяющийся более 1 раза на интервале (1; L). TF ∈ N.
m – одновременное окончание различных тайм-фреймов на интервале (1; L). m ∈ N.
nm – количество одновременных окончаний различных тайм-фреймов на интервале (1; L). n ∈ N.
Ранее было показано распределение nm для TF = 34 на двух интервалах для L1 = 2'200 и L2 = 25'200.
Рассмотрим распределение nm для интервала, в котором L3 = 252'000.
Рост и падение деловой активности формируют подъёмы и спады в экономике, обозначая экономические циклы, состоящие из повторяющихся в экономике рецессий, депрессий и оживлений.
Динамика финансового рынка происходит в корреляции с экономическими циклами. Изменения направлений динамик значений фондовых индексов, котировок валют, стоимости сырья показывают окончания одних экономических циклов и начала других.
В точках, в которых одновременно завершаются тайм-фреймы в годах с 1 по 34 в количестве выше 10 завершений, происходят смены экономических циклов. В окрестностях этих точек во фрактальной структуре графиков динамики стоимости финансовых активов формируются точки бифуркаций, в которых завершаются одни фракталы и начинаются другие.
Для моделирования динамики экономических процессов требуется проведение анализа фрактальных структур графиков, которые построены по следующим годовым тайм-фреймам Фибоначчи:
1, 2, 3, 5, 8, 13, 21, 34, 55 и 10 лет.
Наложение временных отрезков с одновременным завершением большого количества тайм-фреймов с 1 года до 34-го на временные отрезки с одновременным завершением большого количества тайм-фреймов с 1 месяца до 34-го даёт чёткое понимание того, в окрестностях каких точек будут завершаться временные интервалы фракталов самого наивысшего порядка.
Одновременные завершения тайм-фреймов внутри временного интервала происходят в конкретные даты, которые ведут свой отсчёт от начала интервала.
Современное летоисчисление берёт своё начало от года, в котором родился на Земле в человеческом теле в одной из трёх своих ипостаси – Сын Божий, наш Бог Иисус Христос.
Чётких и однозначных фактов, подтверждающих рождение Господа Бога нашего Иисуса Христа именно в тот год, от которого ведётся современное летоисчисление нет. Однако, для Веры и для спасения человеческой души важен не год Рождения, а Непорочное Зачатие и Рождение Иисуса Христа, Его Жизнь и Его Учение, Его Распятие и Его Страдания, Его Воскресение из мертвых и Его Вознесение.
Имеется множество доводов, указывающих на рождение Сына Божия Иисуса Христа на 5 лет раньше, чем это принято считать.
С учётом неопределённости относительно начала современного летоисчисления, для анализа одновременных завершений годовых интервалов с целью выявления временных отрезков, на которых формируются глобальные точки бифуркаций этот факт нужно принимать во внимание.
С учётом этого факта текущий 2021-ый год может быть 2026-ым годом.
Построим годовые тайм-фреймы с 1 по 144 (12²) и найдём временные отрезки, на которых присутствует максимальное количество их одновременных завершений, уделяя при этом особое внимание тем временным отрезкам, где завершаются тайм-фреймы Фибоначчи и обращая внимание на разницу между временными отрезками равную 5 годам.
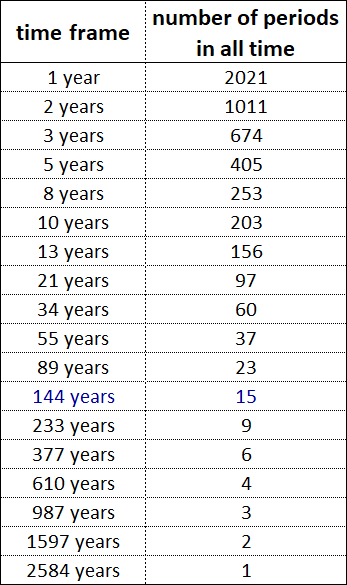
Вершины обозначенных парабол находятся в окрестностях временного интервала с 2021 по 2026 год. С учётом общепринятого времяисчисления верхняя граница диапазона соответствует текущему 2021 году. Если же времяисчисление вести от 5 года до н.э., то текущим годом является 2026, который соответствует нижней границе диапазона.
С учётом отсутствия полной ясности о начале современного летоисчисления, получается ситуация, при которой текущее время находится либо в начале диапазона 2021-2026, либо в его конце.
Временной интервал 2021-2026, в который попадают вершины обозначенных парабол, является интервалом в окрестностях которого завершается максимально возможное количество тайм-фреймов в годах от 1-го до 144-го, что указывает на завершение в этом временном отрезке фракталов высшего порядка.
За временным диапазоном 2021-2026, в окрестностях которого +- 2 года завершается 56 тайм-фреймов, следует 2040-ой год, в котором одновременно завершается 23 тайм-фрейма, что указывает на окончание временных интервалов фракталов наивысших порядков.
2021-2026 – это время начала конца. Начавшиеся в этом периоде фракталы высших порядков к 2040 году завершат фракталы наивысших порядков.
2040 год – это рубежный год, после которого во фрактальных структурах начнут формироваться новые фракталы высших и наивысших порядков.
3.20. Суть метода моделирования.
На этом с временными интервалами можно закончить и завершить теоретическую часть обозначением сути метода моделирования динамики стоимости финансовых активов, которая заключается в выявлении фрактальной структуры графика финансового актива и её описании с помощью аттракторов из азбуки Niro.
Процесс формирования фрактальной структуры аттрактора динамическими фракталами цикличен, а значит прогнозируем, т.е. имеется возможность моделирования будущей динамики котировок любых финансовых инструментов.
В графиках динамики стоимости на финансовом рынке имеется цикл, который заключается в образовании фрактала и выражается в:
1. Формировании 1-го сегмента фрактала.
2. Формировании 2-го сегмента фрактала, направленного в противоположную сторону 1-му.
3. Формировании 3-го сегмента фрактала, имеющего одинаковое направление с 1-ым.
После завершения этого цикла, начинается точно такой же цикл, но в противоположном направлении. Все эти действия продолжаются до бесконечности – первый сегмент всегда сменяется вторым сегментом, второй сегмент всегда сменяется третьим сегментом, а третий сегмент всегда сменяется первым сегментом.
Цикличность процесса формирования фракталов и фрактальной структуры в соответствии с определённым порядком даёт понимание того, какой сегмент фрактала и в каком направлении будет формироваться после того, как завершится формирование текущего сегмента.
В любой момент времени динамика стоимости любого финансового актива пребывает в формировании одного из трёх сегментов фрактала – первого, второго или третьего. После первого сегмента фрактала всегда формируется второй сегмент этого же фрактала, после которого всегда формируется третий сегмент этого же фрактала и затем начинает опять формироваться первый сегмент, но уже другого фрактала, имеющего либо тот же порядок, либо больший, и который обязательно направлен в противоположную сторону предшествующему фракталу.
Точки экстремумов на графике – это точки, в которых либо завершаются первые сегменты и начинаются вторые, либо завершаются вторые сегменты и начинаются третьи, либо завершаются третьи сегменты и начинаются первые. Точки экстремумов определяют границы стоимостных и временных интервалов фракталов во фрактальных структурах аттракторов.
Пропорции между величинами стоимостных и временных интервалов сегментов позволяют определить:
- какими сегментами они являются – первыми, вторыми или третьими,
- какие виды и типы фракталов эти сегменты формируют, и
- каков порядок сформированных фракталов во фрактальной структуре по отношению друг к другу.
Метод моделирования динамики котировок финансовых инструментов построен на определении того, каким является текущий сегмент фрактала – первым, вторым или третьим, чтобы определить каким сегментом фрактала будет следующий после текущего.
Азбука аттракторов Niro состоит из 15 фракталов:
11, 12, 13, 14, 15; 21, 22, 23, 24, 25; 31, 32, 33, 34, 35;
которые поделены на три вида в каждом из которых пять типов.
Каждый из 15 фракталов представляет собой аттрактор, к которому будет стремиться график любой нелинейной динамической системы.
Моделирование будущей динамики стоимости начинается с анализа главной фрактальной структуры, состоящей из фракталов наивысшего порядка, то есть с анализа графиков, построенных по годовым тайм-фреймам. В рамках проведённого анализа главной фрактальной структуры определяется к какому из 15 типов аттракторов относится график динамики стоимости финансового актива.
Идентифицировав аттрактор главной фрактальной структуры, можно делать не только долгосрочные прогнозы динамики стоимости, но и среднесрочные и краткосрочные прогнозы, потому что формирование фрактальных структур, состоящих из фракталов с порядком ниже наивысшего, будет происходить в строгом соответствии и подчинении главной фрактальной структуре.
Таким образом, чтобы ясно видеть будущую динамику финансового рынка, необходимо знать азбуку аттракторов Niro и уметь с её помощью читать и описывать фрактальные структуры графиков финансовых инструментов, торгующихся на валютных, фондовых и товарно-сырьевых рынках.
Азбука Niro исключает апофению из динамики финансового рынка и делает закономерность в динамике стоимости финансовых активов ясной и очевидной. Стать ясновидящим в таком случае под силу каждому.
На этом рассмотрение основных аспектов метода моделирования динамики стоимости на финансовом рынке можно закончить, от теоретической части перейти к практической и рассмотреть применение метода моделирования будущей динамики на конкретном примере.
4. Модель будущей динамики значений индекса Dow Jones.
В качестве примера моделирования будущей динамики возьмём динамику значений американского фондового индекса Dow Jones.
Подробно и детально моделирование динамики индекса Dow Jones рассмотрено в статье “Когда Dow станет Low?”, а здесь приведена уже построенная модель будущей динамики, которая имеет на текущий момент наибольшую вероятность реализации.
В соответствии со сложившейся в конце первого полугодия 2021 года фрактальной структурой графика индекса Dow Jones можно говорить о том, что будущая динамика значений индекса будет проходить в следующем порядке:
1. С 2021 по 2028 год динамика индекса Dow Jones будет нисходящей, в результате которой снижение значений индекса может остановиться на отметке 15’300 пунктов. Такое снижение значений индекса вызвано завершением фрактала 6-го порядка F133313, который является 3-им сегментом фрактала 5-го порядка F13331 и будет происходить в рамках формирования фрактала 5-го порядка F13332, который является 2-ым сегментом фрактала 4-го порядка F1333.
2. С 2028 по 2035 год динамика индекса будет восходящей с целью повторения максимальных значений, которые достигнуты в 2021 году. Такое повышение значений индекса будет происходить в рамках формирования фрактала 5-го порядка F13333, который является 3-им сегментом фрактала 4-го порядка F1333.
3. В 2035 году начнётся глобальное снижение значений индекса Dow Jones в результате одновременного завершения третьих сегментов фракталов разного порядка: F13333, F1333, F133, F13, которые завершат фрактал наивысшего порядка F1. Обвал американского фондового рынка будет проходить на фоне формирования 2-го сегмента фрактала F2 наивысшего порядка. Это снижение может опустить значение индекса Dow Jones к отметке 2’700 пунктов.
С учётом складывающейся локальной фрактальной структуры можно предположить, что внутри временного интервала (1978, 2035) одновременно в 2035 году завершат формирование обозначенные выше четыре фрактала: F1333, F133, F13, F1.
1. Фрактал F1333 является фракталом 4-го порядка, состоит из сегментов: F13331, F13332, F13333, которые являются фракталами 5-го порядка и может представлять собой Fractal №23 из азбуки Niro:
F1333 ≡ F23.
Прогнозируемый временной интервал T1333 – (2014, 2035).
Прогнозируемый стоимостной интервал P1333 = 19750,86.
2. Фрактал F133 является фракталом 3-го порядка, состоит из сегментов: F1331, F1332, F1333, которые являются фракталами 4-го порядка и может представлять собой Fractal №11 из азбуки Niro:
F133 ≡ F11 → FS {13, MS, 23}.
Прогнозируемый временной интервал T133 – (2001, 2035).
Прогнозируемый стоимостной интервал P133 = 27164,66.
3. Фрактал F13 является фракталом 2-го порядка, состоит из сегментов: F131, F132, F133, которые являются фракталами 3-го порядка и может представлять собой Fractal №11 из азбуки Niro:
F13 ≡ F11 → FS {11, MS, 11}.
Прогнозируемый временной интервал T13 – (1978, 2035).
Прогнозируемый стоимостной интервал P13 = 34354,76.
4. Фрактал F1 является фракталом наивысшего 1-го порядка, состоит из сегментов: F11, F12, F13, которые являются фракталами 2-го порядка и может представлять собой Fractal №11 из азбуки Niro:
F1 ≡ F11 → FS {13, 23, 11}.
Прогнозируемый временной интервал T1 – (1896, 2035).
Прогнозируемый стоимостной интервал P1 = 35062,90.
Фрактал 5-го порядка F13331 начал формироваться в октябре 2014 года, а завершил формироваться в мае 2021 года. F13331 является 1-ым сегментом фрактала 4-го порядка F1333, после завершения которого начнёт формироваться фрактал F13332 являющийся 2-ым сегментом фрактала F1333, а далее – фрактал F13333 являющийся 3-им сегментом фрактала F1333.
2-ой сегмент F13332 фрактала F1333, начав формироваться в мае 2021 года, может завершить своё формирование в 2028 году. В рамках формирования фрактала F13332 значения индекса Dow Jones могут опуститься к 2028 году к отметке 16000 пунктов.
3-ий сегмент F13333 фрактала F1333 может сформироваться на временном интервале с 2028 года по 2035 год. В рамках формирования фрактала F13333 значения индекса Dow Jones могут снова подняться из отметки 16000 пунктов к отметке 36000 пунктов.
Фракталы F13333, F1333, F133, F13 являются третьими сегментами фракталов, у которых порядок каждого последующего фрактала выше предыдущего на один порядок.
С завершением фрактала 5-го порядка F13333 произойдёт одновременное завершение и фрактала 4-го порядка F1333 и фрактала 3-го порядка F133 и фрактала 2-го порядка F13 и фрактала наивысшего 1-го порядка F1.
Фрактал 2-го порядка F11 – это 1-ый сегмент фрактала наивысшего 1-го порядка F1. F11 сформировался на временном интервале с 1896 года по 1973 год.
Фрактал 2-го порядка F12 – это 2-ой сегмент фрактала наивысшего 1-го порядка F1. F12 сформировался на временном интервале с 1973 года по 1978 год.
Фрактал 2-го порядка F13 – это 3-ий сегмент фрактала наивысшего 1-го порядка F1. F13 сформируется на временном интервале с 1976 года по 2035 год.
Таким образом, аттрактором фрактальной структуры FS {13, 23, 11} графика индекса Dow Jones является фрактал F11 - фрактал №11 из азбуки Niro, который является 1-го типа и относится к 1-му виду.
Завершение фрактала F13 в 2035 году завершит фрактал F1. Таким образом, начавшийся в 1896 году цикл роста значений индекса Dow Jones завершится.
В 2035 году на американском фондовом рынке начнётся глобальный нисходящий тренд. Падение котировок американских акций может быть настолько сильным, что значение индекса Dow Jones опустится к отметке 2700 пунктов. Данное снижение будет проходить в рамках формирования фрактала наивысшего порядка F2, который является вторым сегментом в глобальной фрактальной структуре.
5. Заключение.
В заключении хочется отметить, что человек, в некотором смысле, является сложной биологической нелинейной динамической системой, продуцирующей другие нелинейные динамические системы, в том числе и такую, как финансовый рынок.
Будущее поведение нелинейных динамических систем является всегда многовариантным, то есть в любой момент времени всегда имеется несколько альтернативных друг другу аттракторов этих систем. Никогда не бывает одного единственного сценария развития тех или иных событий ни в жизни человека, ни на финансовом рынке.
Те события, которые происходят в жизни человека сейчас, и те поступки, которые совершает человек сейчас, определяют соответственно и события, которые произойдут в будущем, и поступки, которые будут в этом будущем им совершаться.
Те колебания стоимости на финансовом рынке, которые происходят сейчас и те фракталы, которые формируются на графиках финансовых активов сейчас, напрямую определяют будущую их динамику.
Мозг человека – это биологический компьютер, функционирующий в строгом соответствии с загруженными в него программами и алгоритмами, которые формируют определяющие его жизнь мировоззрение, взгляды, поступки, действия.
Метод моделирования стоимости на финансовом рынке, о котором шла речь выше, можно считать некой компьютерной программой, ну или неким алгоритмом, “загрузив” свой мозг которым, можно увидеть и понять, что на финансовом рынке ничего случайного и хаотического не происходит и что динамика котировок финансовых активов упорядочена и определена формирующим фрактал-аттракторы оператором N.
 — Бесплатные Сайты и CRM.
— Бесплатные Сайты и CRM.